
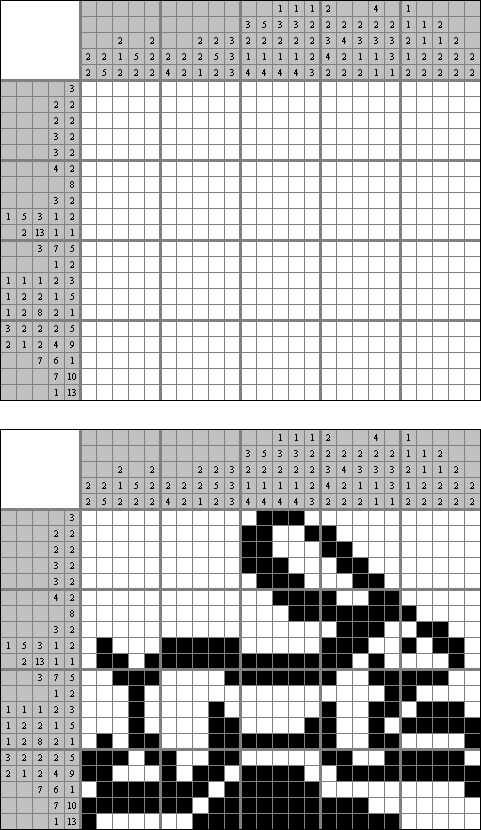
Cross+A 软件是一种能措置各式各种谜题的软件。软件复古谜题的成批处理。
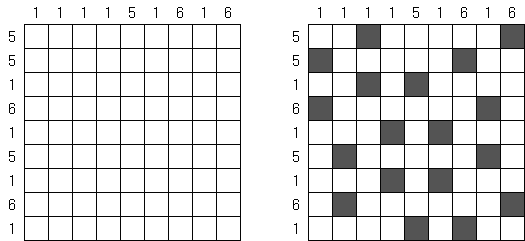
以数绘画(Nonogram) 数和(Kakuro) 数壹(Hitori) 数回(Slitherlink) 像素迷惑(Link-a-Pix) 像素填空(Fill-a-Pix) 军舰(Battleships) 数桥(Hashiwokakero) 珍珠(Masyu) 点灯(Light Up) 码牌(Fillomino) 不等式(Futoshiki) 数暗(Kuromasu) 数墙(Nurikabe) 角尺数墙(Sashikabe) 数矢数墙(Yajikabe) 帐篷(Tents) 算独(Calcudoku) 嗨达图(Hidato) 数蛇(Numbrix) 数方(Shikaku) 星系(Galaxies) 摩天楼(Skyscrapers) 数波(Hakyuu) 伟大旅行(Grand Tour) 易如ABC (Easy as ABC) 云朵(Clouds) 数矢(Yajilin) 扫雷(Minesweeper) 扫雷军舰(Minesweeper Battleships) 数间(Heyawake) 十格(Tenner Grid) 一百(Hundred) 箭头(Arrows) 数学数独(Mathrax) 顺独(Str8ts) 扫线(Linesweeper) 二元(Binairo) 墙壁(Walls) 数邻(Dominosa) 拼布(Patchwork) 克诺索斯(Knossos) 矩形(Rekuto) 邻居(Neighbours) 四风(Four Winds) 留方(Shakashaka) 方阵和(Kakurasu) 麻糬染色(Mochikoro) 看穿(Seethrough) 灯塔(Lighthouses) 灯塔军舰(Lighthouse Battleships) 塔帕(Tapa) 禁制四(Fobidoshi) 岛屿(Island) 版图(Dominion) 泊车场(Tren) 无四连气儿(No Four in a Row) 畜栏(Corral) 四个方格(Foseruzu) 直线交叉(Sutoreto) 连气儿数字(Renban) 亮光(Buraitoraito) 插画(Irasuto) 数字块(Suguru) 三努多(Trinudo) 溪流(Creek) 盖比(Gappy) 趣味昂贵(Norinori) 四格分割(Yonmasu) 砖块(Bricks) 数字链(Number Chain) 摆放地毯(Kapetto) 连胜(Renkatsu) 希腊拉丁方阵(Eulero) 不同马赛克(Anraikumozaiku) 玄色单位(Kurotto) 寻找方块(Tasukuea) 星际大战(Star Battle) 真金不怕火狱(Araf) 弯说念(Kabingurodo) 温度计(Thermometers) 长蛇(Snake) 喷涂区域(Peintoeria) I形环路(Irupu) 角尺(Sashigane) 数字角尺(Sashikazune) 巧克力(Chocona) 相邻相异(Different Neighbours) LITS骨牌(LITS) 数字球(Nanbaboru) 地砖喷涂(Tairupeinto) 阴阳(Yin-Yang) 数途(Nanro) 光与影(Light and Shadow) 数连(Arukone) 俄罗斯方块密铺(Tetroid) 舛误块(Sukima) 三胞胎(Triplets) 正确迷惑(Korekutokonekuto) 双重块(Doppelblock) 目田三(Furisuri) 山羊和狼(Yagit) 隧说念环路(Purenrupu) 填充榻榻米(Firumatto) 领地(Nawabari) 马卡罗(Makaro) 千里浮(Dosun-Fuwari) 回家(Satogaeri) 科布林(Koburin) 差一数和数独(Sukrokuro) 白黑(Shirokuro) 罗马(Roma) 范畴块(Bodaburokku) 玄色射击(Kuroshuto) 远处誓词(Toichika) 撒谎榻榻米(Usotatami) 管说念迷惑(Pipelink) 盒装(Hakoiri) 绘画棒(Nuribou) 榻榻米加工(Tatamibari) 日与月(Sun and Moon) 贡献(Kojun) 一个坏话(Usowan) 数斜(Gokigen Naname) 蛇一五(Hebi-Ichigo) 移动(Hamle) 玉石(Gyokuseki) 镜公馆(Kin-Kon-Kan) 位置(Ichimaga) 岛国(Shimaguni) 牧场(Meadows) 箭头和数字(Yajisan-Kazusan) 蛇穴(Snake Pit) 捡起石头(Hiroimono) 灌水(Water Fun) 来回(Round Trip) 数字交叉(Number Cross) 三和一(Santoitchi) 火腿三明治(Hamusando) 跟踪数字(Trace Numbers) 地区画分(Area Division) 数子(Sukoro) 收支(EntryExit) 登入(Sign In) 瑕瑜环路(Kuroshiro) 月亮或太阳(Moonsun) 矩形滑块(Rectslider) 石上石(Stostone) 咖啡牛奶(Kohi Gyunyu) 奶茶(Mirukuti) 斜线打包(Slash Pack) 绘画迷宫(Nurimaze) 运河抖擞(Canal View) 乡间小径(Country Road) 不是团子(Nondango) 排球(Mintonette) 箭头迷宫(Arrow Maze) 箭头收罗(Arrow Web) 分离组合(Hanare) 绿洲(Oases) 兔子和树(Rabbits and Trees) 星星和箭头(Stars and Arrows) 特等环线(Kanjo) 看空气(Rukkuea) 蛇岛(Golem Grad) 三部曲(Trilogy) 等第(Grades) 覆面墙(Hukuwall) 绘图大氅(Nurimisaki) 星夜(Starry Night) 调换与不同(Douieru) 四格骨牌(Tetoron) 矩形宽高差(Sashikaku) 六格(Heki) 城墙(Castle Wall) 死角(Deddoanguru) 异常线(Endorain) 真金不怕火狱数墙(Nuraf) 说念路(Miti) 箭流(Arofuro) 每隔一行弯(Every Second Turn) 可动性(Mobiriti) 移动数(Mubunanba) 地皮十(Terra X) 远处旯旮(Rimotoejji) 折返(Double Back) 蠕虫(Wamuzu) 咱们回家吧(Kaero) 闭合(Kapama) 唯一绚丽(Yunikumaka) 弯曲数字(Meandering Numbers) 容器分割(Yokibunkatsu) 屏幕(Scrin) 从 1 到 X (From 1 To X) 交通灯(Shingoki) 缝合(Stitches) 相邻骨牌(Neibadomino) 杰米尼(Jemini) 双重巧克力(Double Choco) 拐角环路(Konarupu) 指点箭头(Gaidoaro) 中点环路(Mid-Loop) 哪个环路(Dotchi-Loop) 三元(Trinairo) 绕行(Detour) 均衡环路(Balance Loop) 草皮(Turf) 方框与圆圈(SquarO) 合页(Chiyotsui) 埃卡(Aqre) 直线环路(Geradeweg) 玄色克隆(Kuroclone) 箭头推箱子(Yajisan-Sokoban) 线段(Line Segment) 野猫舆图(Raneko) 寻找因子(Factorism) 群岛(Akiperago) 连数填字(Yakazu) 镜像瓷砖(Miraringutairu) 数间方块(Heyablock) 巧克力香蕉(Choco Banana) 候鸟(Wataridori) 链条块(Chenburo) 一室一门(Wanrumuwandoa) 屋子(Haisu) 轨说念(Obitaru) 正方密铺(Square Jam) 鸡尾酒灯(Cocktail Lamp) 家眷写照(Kazoku) 均等房间(Tontonbeya) 荆棘文(Context)Nonogram (数图,"Hanjie", "Paint By Numbers", "Griddler","CrossPix") 谜题的盘面是个正方形或长方形,它的主义是字据给出的数字赢得一幅风趣无尽的简笔画;左边和上头的数字过火数量指出在相应的线上每个聚合的玄色方格数量和玄色方格聚合的数量。玄色方格聚合中间一定有最少一个空方格。
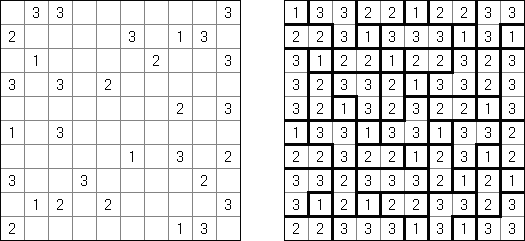
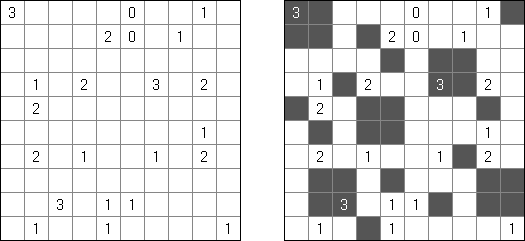
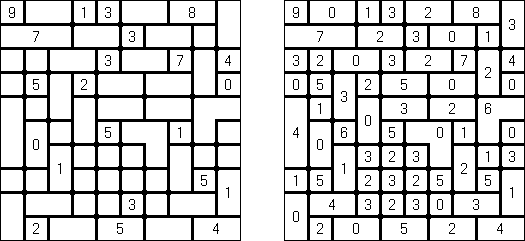
Kakuro (数谜,"Cross Sums") 是一种数字谜题,亦然纵横字谜的数学模拟体。需要将1至9数字填入方格中,有的方格无法填上(玄色方格)。在包含数字的玄色方格中上头的数字暗示在该方格右边白色方格的数字之和,而在玄色方格中底下的数字暗示在该方格底下白色方格的数字之和。比如,"6"数字是1+5 或2+4之和;不得填上合并的数字(3+3)。
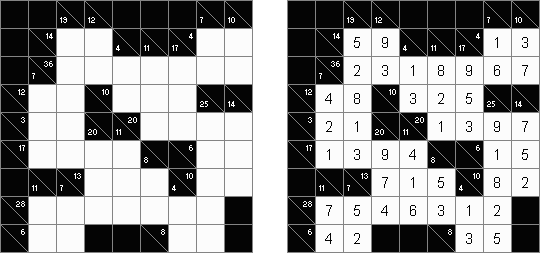
Hitori ("单独")是一种逻辑谜题。需要将重复的数字涂黑,数字在职何行或列里不重复。涂黑的方格只能用格角毗邻,不不错用方格的侧边毗邻。未涂黑的小格要组成联翩而至的白色空间,白色方格与白色方格之间必须相连。
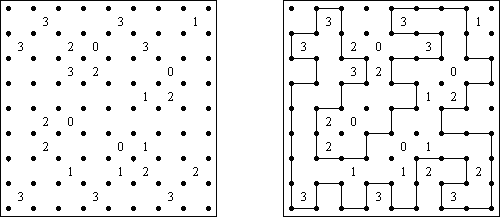
Slitherlink (数回,"Fences", "Loop the Loop", "Dotty Dilemma","Sli-Lin")是一种逻辑谜题,与迷宫相似。需要用纵线段和横线段将圆点迷惑起来以组成一条不远隔而不交叉的回路。每个数字相当于该数字四周的线段数量。若是在方格中没罕有字,那么该方格四周的线段数量不限。
Link-a-Pix ("Paint by Pairs")是一种数字谜题。在格网里除了1数字除外齐有重复的数字。需要将成对的数字用一条线迷惑起来,而且该条线通过的方格数量要相当于该条线开首和异常的数字。迷惑的线不错是弧线,并将数字水平或垂直地迷惑起来(可是对角线场所不允许),而且折线不得交叉或历程合并个方格。

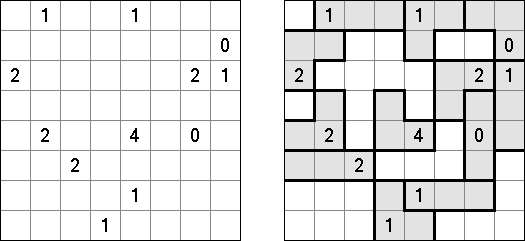
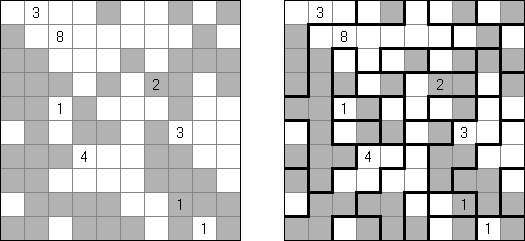
Fill-a-Pix ("Mosaic", "Magipic", "Nurie Puzzle", "Fill-In") 是一种用数字拼图的逻辑谜题。每个数字指出要涂黑若干贯串的方格(包括该数字的方格),比如,若是在方格中有"0"数字,那这个方格过火贯串的方格齐不需要涂黑。
Battleships (军舰游戏,"Solitaire Battleships", "Battleship Solitaire") 是一种谜题,其划定和一款著明的游戏相似。需要在盘面上摆放"船舰",主要要求是"船舰"在对角和邻边齐不不错相邻。右边和底下的数字暗示在相应的行或列里有几个"船舰"的部分。

Battleships圭表盘面是10×10。在例子中有一个占据4个方格的"船舰",两个占据3个方格的"船舰",三分占据2个方格的"船舰"和四个占据1个方格的"船舰"。就怕"船舰"有的部分已知。
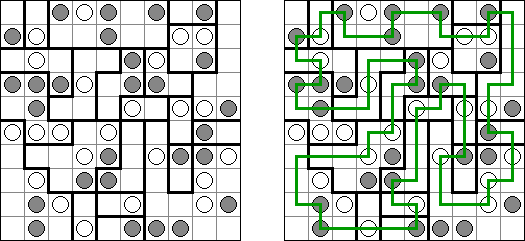
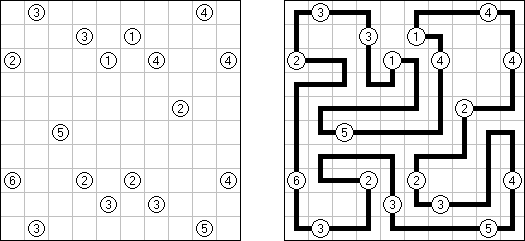
Hashiwokakero ("桥梁"或"筷子","Hashi", "Bridges", "Chopsticks", "Ai-Ki-Ai") 是一种谜题,需要将包含数字的圆圈(孤岛)用直线("桥梁")迷惑起来。每座岛的数字暗示要架到该岛的桥梁的数量;通盘的岛要相互重迭,不错从一座岛通过桥梁达到任何岛。
两座岛中间的桥梁数量不得实足2座,不错水平或垂直地划条线(对角线场所不允许),条线不得对折起来或相交叉或聚积岛。
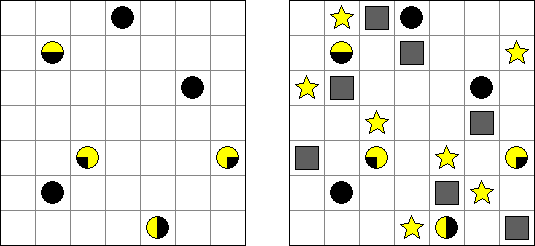
Masyu ("Shiroshinju Kuroshinju", "White Pearls and Black Pearls") 是一种逻辑谜题,需要将白色和玄色的圆圈用横线和竖线迷惑起来以组成一条不交叉的回路。这条线要胜利通过白圆圈,并在前一个或后一个方格中(或在这两个方格中)改革场所。这条线通过黑圆圈时,要在包含黑圆圈的方格里改革场所,在前一个或后一个方格中不得折起来。
Light Up (点灯,"Akari", "Bijutsukan") 是一种逻辑谜题。盘面分为白色方格和玄色方格,其中有的玄色方格包含数字。需要将"灯"摆放在白色方格中,以"照亮"全盘面,但"灯"不得互相"照亮"。
"灯"不错横向或纵向地发光,但也不错由玄色方格撅断。在玄色方格中不错有一个0至4的数字,其暗示该方格周围有若干"灯"(不包括在该玄色方格的斜对方进取摆放的"灯")。若是方格不包含数字,那在其周围上不错摆放的"灯"数量不限。
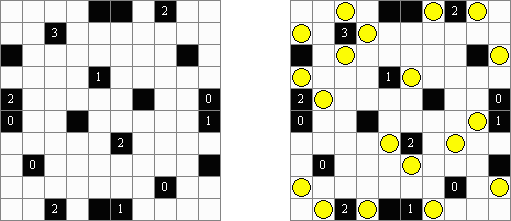
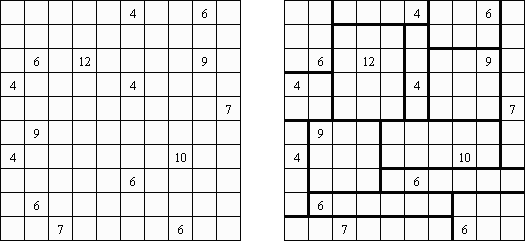
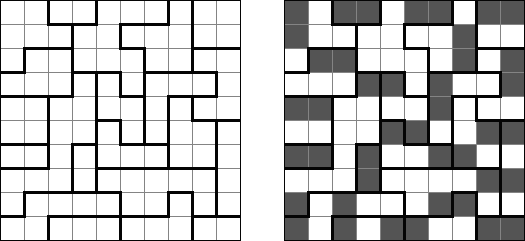
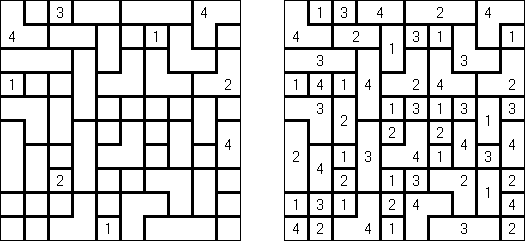
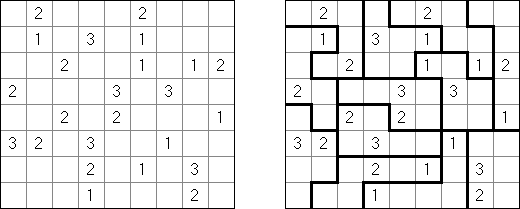
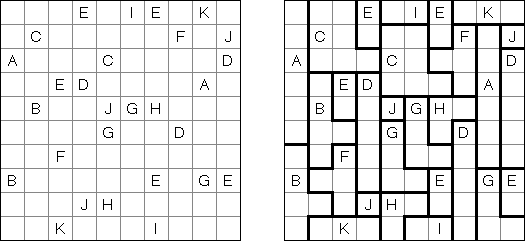
Fillomino ("Polyominous")谜题的盘面是大小松弛的长方形格网,在有的小格中罕有字。需要将盘面分为几个大块,每个大块包含的小格数量要相当于大块的小格包含的数字。大小调换的大块不不错水平或垂直地相连。不包含数字的小格也不错组成大块,有助于措置该谜题。
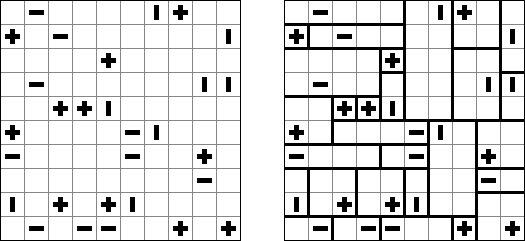
Futoshiki ("不等式", "Hutoshiki", "Unequal") 是一种数字谜题。盘面是正方形格网,在有的小格中罕有字;小格中间不错有"<" 和 ">"象征,这两种象征暗示贯串的数字大小对比。需要将数字填入空方格中,而且数字在每行及列里不成重复。
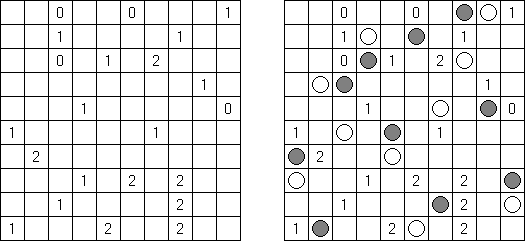
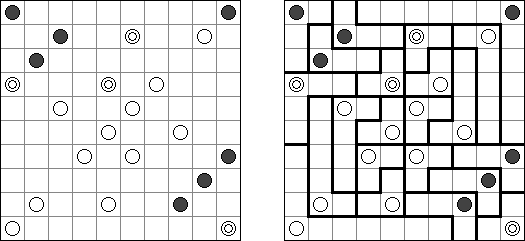
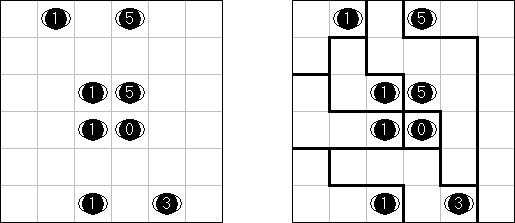
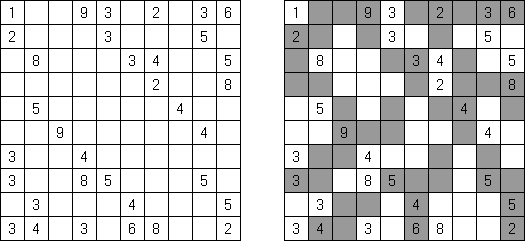
Kuromasu ("Kurodoko", "Where is Black Cells?") 谜题的盘面是长方形格网,有的方格包含数字。需要按照以下要求将方格涂黑:
每个数字表明了该方格为开首的横向和纵向的白色方格数量;白色方格的数量会由玄色方格或盘面的旯旮为止; 包含数字的方格一定是白色的; 玄色方格在横向和纵向齐不得相连; 通盘的白色方格在横向能够纵进取必须是连气儿的,而且组成一个白色的空间。
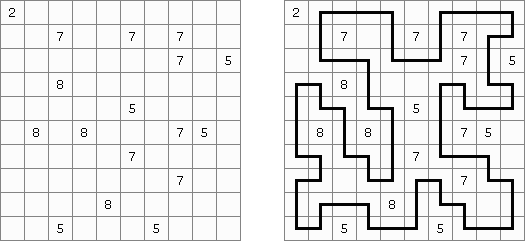
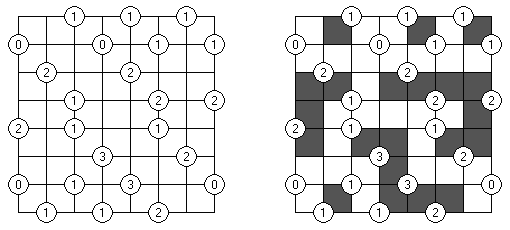
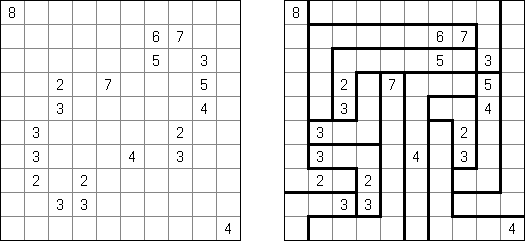
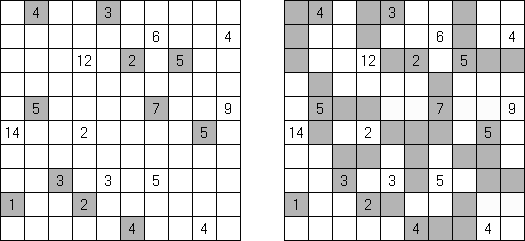
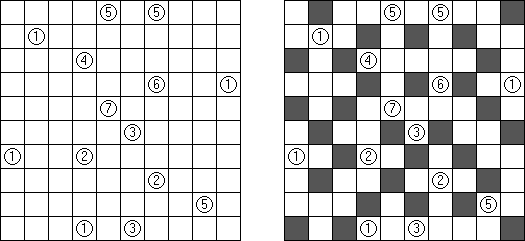
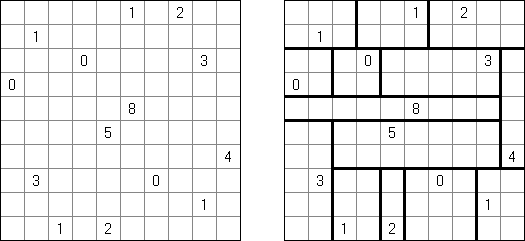
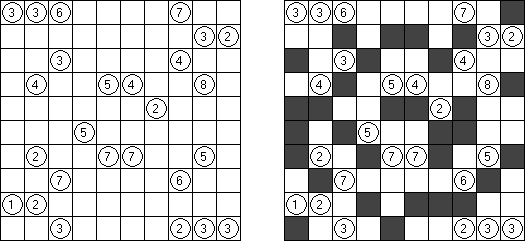
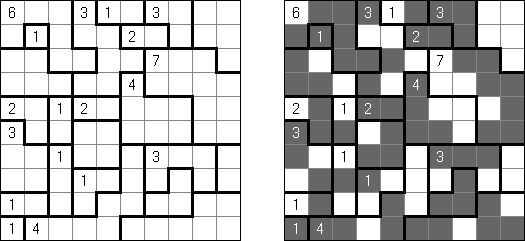
Nurikabe (数墙或"神奇笔刷", "Cell Structure", "Islands in the Stream") 是一种数字谜题。在日本外传中,"Nurikabe"是一面隐形的墙,它会阻档旅东说念主的路,使东说念主迷失场所。
需要按照以下划定复原岛位置的舆图:
每个数字指出相应的岛占据若干方格; 任何两座岛只能用对角相连; 每座岛只包含一个数字; 岛之间有一条河(玄色方格的聚合); 玄色方格要相迷惑起来; 玄色方格不得造成2×2的正方形。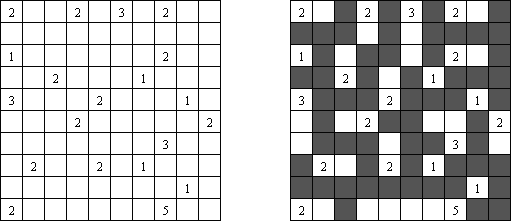
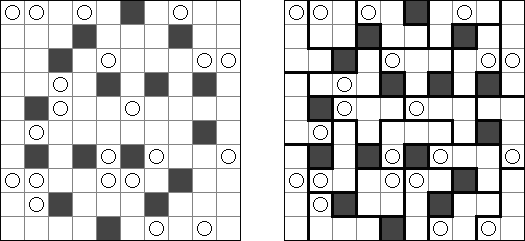
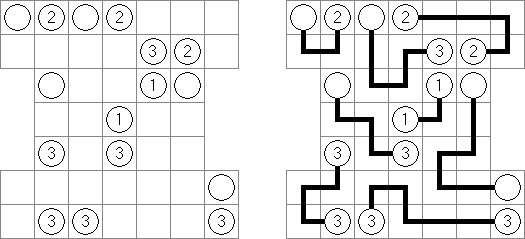
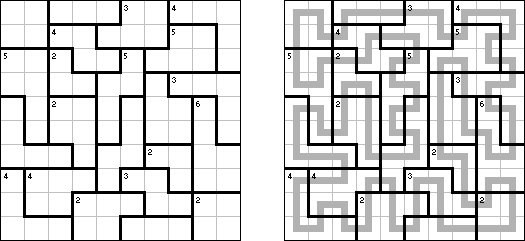
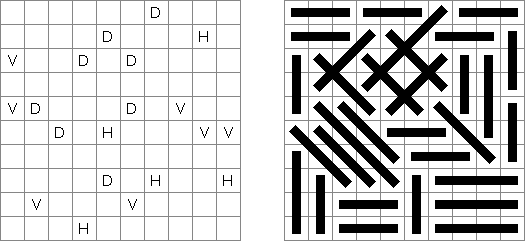
Sashikabe combines Nurikabe puzzle with Sashigane puzzle. The goal is to blacken some cells of a grid according to the following rules:
All of the black cells must be connected. There cannot be any 2 x 2 blocks of black cells. All islands must be L-shaped and one cell wide. Two islands may not be connected. A circle represents a cell in which an "L" must bend. An island must have the same number of white cells as a number in a circle. An arrow marks the end of the island's "leg"; the arrow points to the cell in which the "L" bends.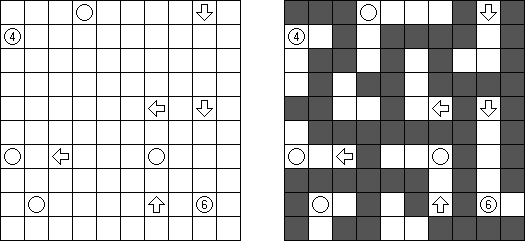
Yajikabe was invented by Naoki Inaba (Japan): he combined Yajilin and Nurikabe puzzles. The goal is to blacken some cells of a grid according to the following rules:
Cells with numbers are always white. No 2 x 2 cell area within the grid can contain all black cells. All the black cells form one contiguous region. A cell containing a number and an arrow represents how many black cells are in the row or column pointed at by the arrow.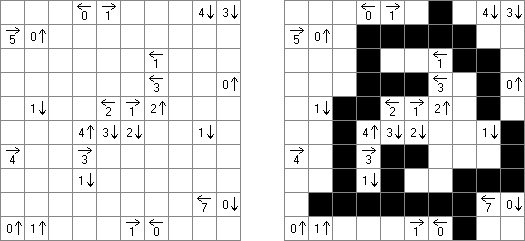
Tents ("搭帐篷", "Tents and Trees")谜题的盘面是长方形格网,有的方格包含"树"。需要按照以下划定在"树"周围上搭帐篷:
帐篷的数量相当于树的数量; 只能在相应的树上水平或垂直地打帐篷,对角场所不准; 两个帐篷不得在相邻能够对角的位置摆放; 左边和上头的数字指出在相应的行或列里要打若干帐篷。
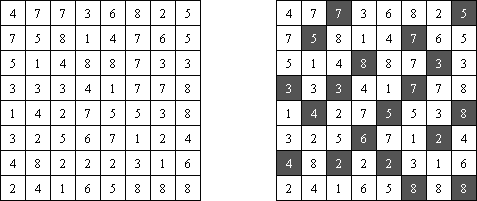
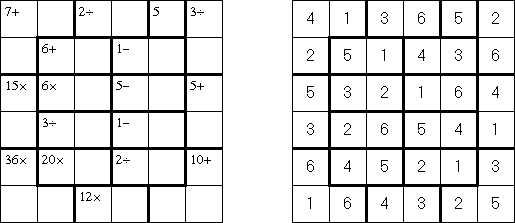
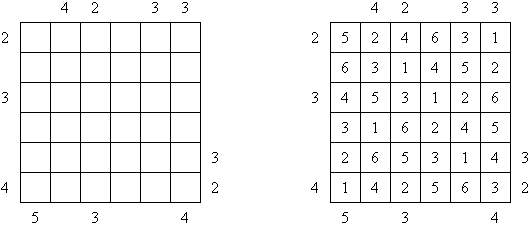
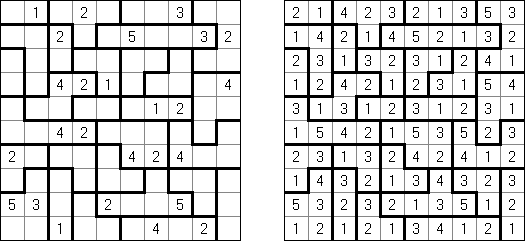
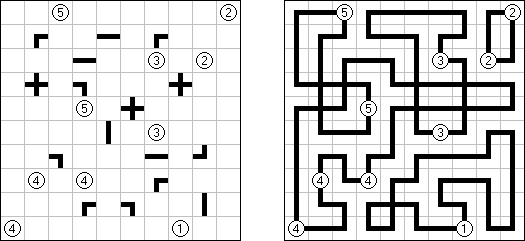
Calcudoku (贤贤, "KenKen", "KENKEN", "KenDoku", "Square Wisdom") 是一种数学逻辑谜题。需要将数字填入格网,在每行和每列里不成重复。每个粗线条围成的区域上角的数字是该区域里的数字算术的后果。与Killer Sudoku比较,这种谜题中在区域里的数字不错重复。
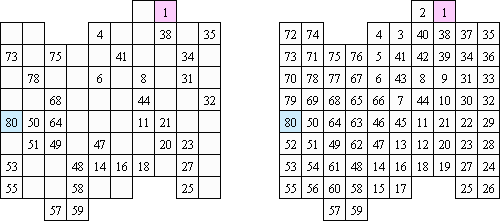
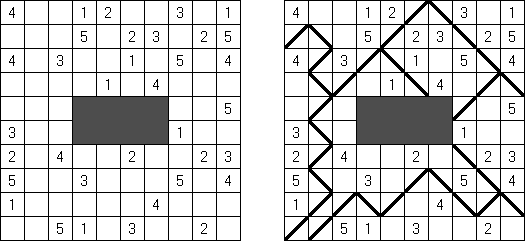
Hidato (意第绪语:"我的谜题")谜题由以色列数学家Gyora Benedek制作。Hidato的盘面是松弛阵势的格网(一般是长方形或正方形)。主义是水平或垂直或斜对地填上连气儿的数字。在格网中有已知的最一丝和最大数。另外,在盘面上还会给出其它的数字,来裁汰谜面的难度,而且保证谜面唯有唯一的解法。
Numbrix是一种逻辑谜题。在长方形格网中有已知的数字,需要将连气儿的数字水善良垂直地填入空的方格,对角的场所不准填入。
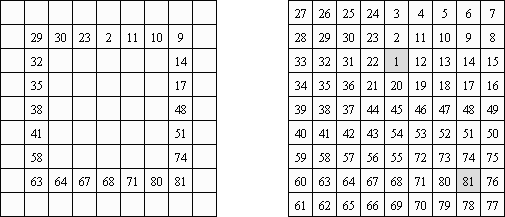
Shikaku (数方或"方形的切口", "Divide by Squares", "Divide by Box", "Number Area") 是一种逻辑谜题。其盘面是松弛大小的长方形格网,有的方格包含已知的数字。划定是:需要划出粗的线使全格网分为长方形或正方形的"区域",每个"区域"要包含一个数字,数字要即是该"区域"占据方格的数量。
Galaxies ("星系", "Tentai Show") 是一种波及逻辑学和几何学的谜题。需要将包含圆圈的长方形格网分为"区域";每个"区域"只能包含一个圆圈,而且圆圈要处在"区域"的对称中心。
Skyscrapers ("摩天楼")是一种逻辑谜题。策动是在格网中填上数字,数字在每行和每列里不得重复。要填上的数字暗示在方格中的楼有若干层;格网对外的数字指出能看到几个在相应的行或列里的楼(比如,由于六层楼,无法看到下一个四层楼)。
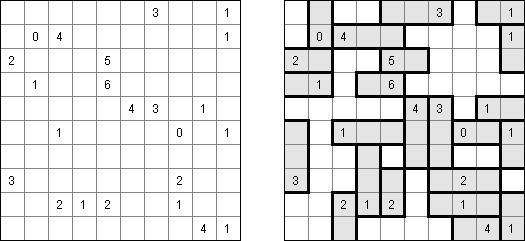
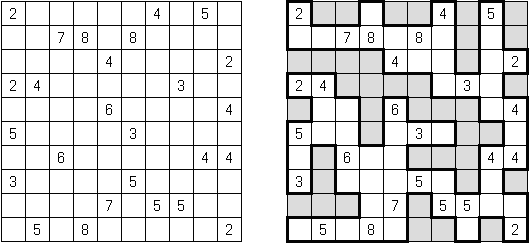
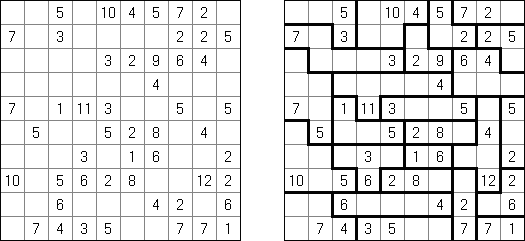
Hakyuu ("波纹作用", "Ripple Effect", "Seismic") 是一种逻辑谜题。长方形格网分为大块("房间"),在有的小格中罕有字。需要在通盘的小格中填上数字使每个大块齐包含1到与该大块所占据的方格数量至极的数字。若是在某行或列里有两个重复的数字,那重复的数字之间的小格数量要即是或大于该数字。比如,一列里有两个包含"5"数字的小格,它们之间的小格数量要即是或大于5。

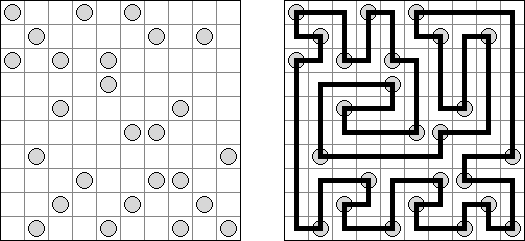
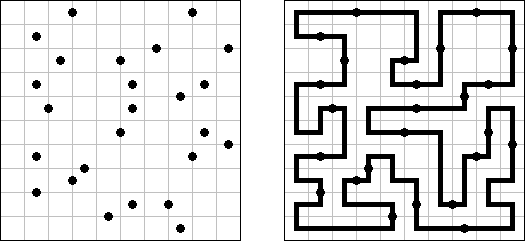
Grand Tour ("伟大的旅行") 是一种逻辑谜题。需要在长方形或正方形格网中将通盘的圆点用一条不交叉的回路迷惑起来。为了保证谜面的解法的唯一性,有的圆点已用线段迷惑。
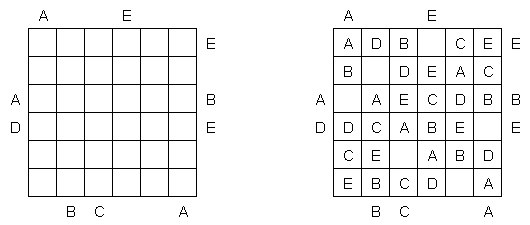
Easy as ABC ("跟"ABC"一样简易", "ABC End View", "Last Man Standing")是一种包含字母的逻辑谜题。需要在正方形方格中填上拉丁字母(比如,A至E),每个字母在每行或每列里不成重复。在方格中不错留空的小格;方格外的字母表明将该字母要摆放在相应的行或列的第一个方格中。
Clouds ("云", "Radar")是Battleships谜题的种类。需要在松弛阵势的格网中将方格涂黑块("云"),"云"在相邻能够对角场所不得相连。方格右边和底下的数字指出"云"占据的方格数量;"云"的数量和大小未知,已知的是"云"侧面占据的方格数量即是或大于2个。
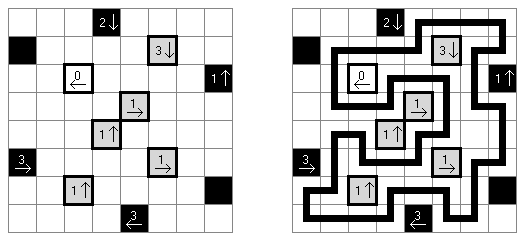
Yajilin ("箭头圆环","Arrow Ring","Straight and Arrow") 是一种逻辑谜题。在正方形或长方形格网中罕有字和箭头象征,它们指出玄色方格在格网中的位置。谜题的策动是画一条不交叉而欠亨过包含箭头的方格或玄色方格的回路。 The grid may contain gray cells that can not be part of the loop.
箭头和数字指出在哪个场所的行或列里有若干玄色方格; 闭合线只能通过不包含数字和箭头的白色方格; 在方格中的数字指出玄色方格的数量,比如,方格包含的"3"数字和往左指的箭头暗示在该方格左边有三个玄色方格; 玄色方格在水善良垂直场所不得相连; 在格网中可能有未用箭头表明场所的玄色方格。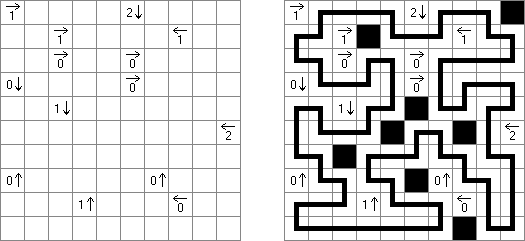
Minesweeper (扫雷)是一种Microsoft Windows操作系统用户齐知的游戏。需要按照数字在空的方格中布雷。每个数字指出了隔壁区域中地雷的数量。一个方格能包含一个地雷,在包含数字的方格中不布雷。
Minesweeper Battleships ("扫雷军舰", "Battlemines")结合了两款流行的谜题游戏。需要在盘面上摆放"船舰", "船舰"在对角齐不不错相邻。方格的数字表明在该方格周围(包括对角)有几个"船舰"。
Heyawake (数间)是一种逻辑谜题。长方形格网分为大块("房间"),其中有的大块包含数字;数字指出该大块要占据的玄色方格数量。若是在大块中没罕有字,该大块占据的玄色方格数量不限。
玄色方格只能对角相连; 通盘的白色方格需要水平或垂直地相迷惑起来; 白色方格的相连数量不得通过两个以上的"房间"。
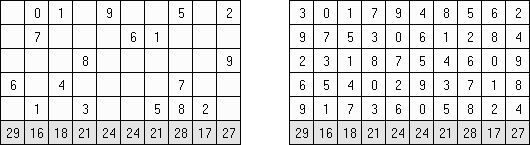
Tenner Grid ("From 1 to 10", "Zehnergitter", "Grid Ten") 谜面是宽度即是10个方格的长方形格网。需要填入格网使每行包含1至9的数字,在列里数字不错重复。格网底下的数字表明该列内部所罕有字之和。在横向相邻的方格中(包括对角场所的方格)数字不得重复。
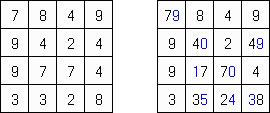
Hundred ("一百")谜题中,正方形格网的每个小格齐罕有字,需要加上数字使每行和列里的数字之和即是一百。
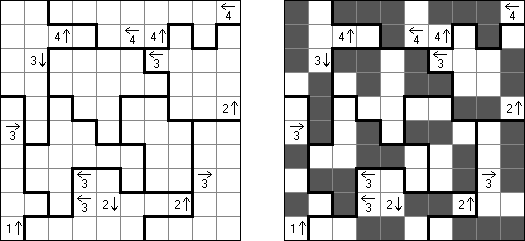
Arrows ("箭头")是一种逻辑谜题。长方形或正方形的格网罕有字。谜题的策动是在格网外面摆放箭头;每个箭头最少要指令一个包含数字的方格,数字暗示指向该方格的箭头数量。
Mathrax亦然一种逻辑谜题。需要在正方形的格网中填上数字,在每行和每列里不重复。有的方格有已知的数字,而且格网中也可能有暗示底下要求的圆圈:
圆圈里的数字和算术象征指出在对角线场所和相邻的方格中两个数字的算术后果; 拉丁字母"E"指出在圆圈周围的四个数字齐是偶数("E"是英文"even",偶数); 拉丁字母"O"指出圆圈周围的四个数字齐是奇数("O"是英文"odd",奇数)。
Str8ts (顺独, "Straights"是扑克术语)是一加拿大东说念主Jeff Widderich制作的种逻辑谜题。正方形的格网分为玄色和白色的方格,需要在白色方格中填上连气儿数字,数字不需要按从大到小的限定摆设(比如,2-1-3-4)。在白色方格和玄色方格中的数字在每行或每列里不得重复。连气儿数字组不包括玄色方格的数字。

Linesweeper是一种逻辑谜题,其划定和扫雷谜题相似。在正方形或长方形的格网中有的方格罕有字(0至8)。需要整齐条通过方格的不交叉的回路,它不得通过包含数字的方格。数字指出那条线通过该数字周围的方格的数量。
Binairo (二元的谜题, "Binary Puzzle", "Takuzu", "Tohu wa Vohu") 是一种使用"0"和"1"数字的逻辑谜题。需要按照以下划定将数字填入长方形或正方形的格网中:
在每行和每列里的"0"数量即是于"1"数量。 数字不得在两个以上相邻的方格中重复; 在每行和每列里数的限定必须是惟一无二的。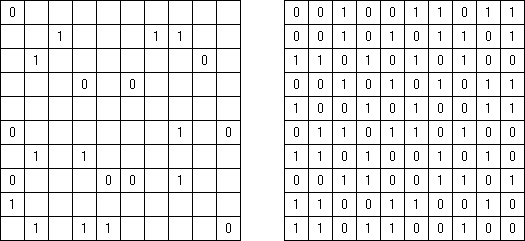
Walls ("墙")是一种逻辑谜题,是由日本东说念主Naoki Inaba发明的。需要在白色方格中划出水平线和垂直线使从玄色方格中发出的线总长度与玄色方格中的数字相符。

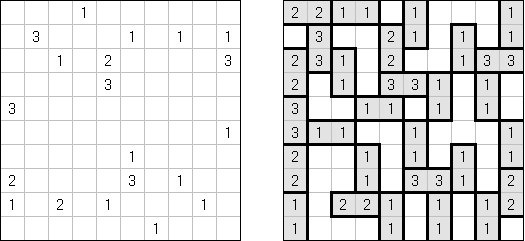
Dominosa ("数邻", "Dominosa Omnibus", "Solitaire Dominoes", "Domino Hunt")是一种使用多米诺骨牌的逻辑谜题。在盘面上唯罕有字;需要"复原"骨牌之间的界线。
Patchwork ("帕奇维克","Tatami")是一种将格网分为一样尺寸的地区("房间")的谜题。需要在每个房间摆放数字,数字要即是从1至该房间包含的方格数量。每列和每排要包含每个数字的一样数量。水平或垂直相邻方格的数字不得重复。
这种谜题还不错使用字母代替数字。字母和数字的谜题Cross+A软件齐能解答。
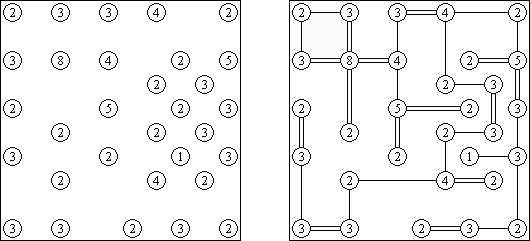
Knossos ("克诺索斯"是克里特岛上的古城和王宫,也动作米诺陶洛斯被关进的迷宫所在地)是一种谜题,在长方形或正方形格网里的几个方格罕有字。需要将格网分为地区("房间")使每个地区唯有一个数字。这个数字要相当于该"地区"周长。
Rekuto是正方形或长方形格网的逻辑谜题。有的方格罕有字。需要划出将格网分为长方形和方形地区的粗线使每个地区只包含一个数字,这个数字要即是该地区的宽度和高度的总额。
Neighbours ("邻居")是一种苟且阵势格网的逻辑谜题。有的方格包含数字或问号。需要将格网分为地区,每个地区的方格数量至极。每个地区只能以有一个包含数字(问号)的方格;这个数字表明该地区有几个"邻居"。若是两个地区有共同的界线,那算是邻居。若是地区有包含问号的方格,该地区的"邻居"数量不限。

Four Winds ("四风", "Line Game")是一种逻辑谜题,正方形或长方形的格网有玄色和白色的方格。需要划出直线,那些直线要从玄色方格起程并历程通盘白色方格。在玄色方格中的数字表明那些直线占据几个白色方格。直线不得交叉。

Shakashaka("摇一摇", "Proof of Quilt")是一种逻辑谜题,正方形或长方形的格网有白色和玄色的方格;其中玄色方格罕有字(0至4)。需要在白色方格中摆放玄色三角形以造成白色的长方形和正方形。有的白色方格不错留空。那些地区不错有水平、垂直或斜对的位置。驾御的白色地区不得有共同的面。玄色方格的数字表明有几个三角形与该方格接邻。

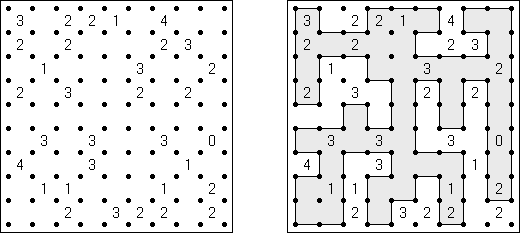
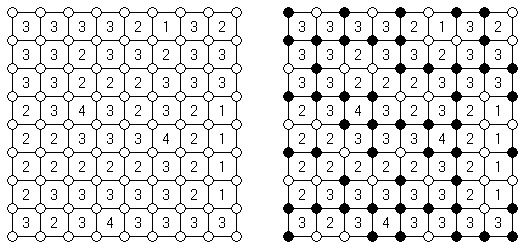
Kakurasu ("Index Sums") 是一种逻辑谜题,需要在正方形或长方形的格网中划出白色和玄色的方格。处在格网左边及上头的数字表明在行和列中的玄色方格"分量"之和。处在格网右边及底下的数字指明在相应的行和列中的玄色方格的"分量"(第一行和第一列的玄色方格的"分量"即是1,第二行和第二列的玄色方格的"分量"即是2, 等等)。
Mochikoro ("Mochinuri") 逻辑谜题使用长方形或正方形的格网,几个方格罕有字。需要通过划出白色方格和玄色方格的情势造成白色方格组成的长方形或正方形的"岛"。
每个"岛"只能以有一个含数字的方格。该数字表明组成这个"岛"的白色方格数量; 有的"岛"莫得含数字的方格; 白色的区域不得斗争侧面,而是在对角斗争; 在格网中不得有2×2的玄色方格组成的区域。
Seethrough ("看穿", "Doors", "Open Office") 是一种逻辑谜题,正方形或长方形的格网中的每个方格表明"房间"。需要关或开房间之间的"门"。掀开的门让从一个房间看到另一个房间或看穿几个房间。在方格中的数字表明从这个房间能看到的房间数量(不算该房间)。在格网中的部分齐不得单独,从任何房间能到任何房间。
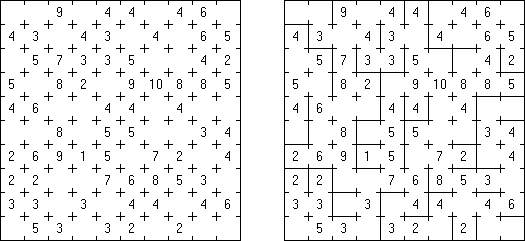
Lighthouses ("灯塔")是一种逻辑谜题,在格网中有包含数字的玄色方格("灯塔")。数字表明该灯塔照亮的船舶数量。灯塔照亮的船舶处在该灯塔的行或列中,在灯塔和船舶之间不错有其他船舶及灯塔。每个船舶由至少一个灯塔照亮。船舶不得斗争到任何灯塔或其他船舶,在对角也不得斗争。
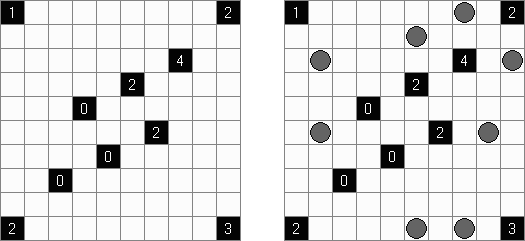
Lighthouse Battleships combines Battleships with Lighthouses puzzle. A cell with a number is a lighthouse, and it indicates the total number of ship pieces that are in the same row or column as the lighthouse. Ships can not touch the lighthouses, not even diagonally.
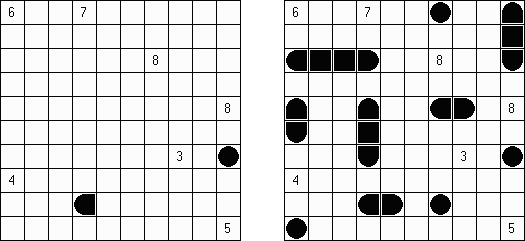
Tapa 逻辑谜题,是由土耳其东说念主Serkan Yurekli发明的。这种谜题使用正方形或长方形的白色格网。需要恪守以下要求用玄色涂上方格:
通盘的玄色方格要在水平或垂直的场所互相斗争; 不得有2×2的玄色方格组成的区域; 几个方格包含数字或问号;这些方格不要涂上; 每个数字表明该白色方格周围的一连串玄色方格的数量;这么的玄色方格群之间要有至少一个白色方格; 问号表明0以上的任何数字; 在方格内部的数字位置及限定不起作用。
Fobidoshi ("Forbidden Four") 是一种由日本东说念主Naoki Inaba发明的逻辑谜题。使用长方形或正方形的格网,几个方格有小圆圈。需要将小圆圈放在空的方格中,小圆圈要在水平或垂直的场所互相斗争。水平或垂直地斗争的小圆圈数量不得超于4个。

Island ("岛", "Tents Island", "Airando")是一种逻辑谜题,是由日本东说念主Naoki Inaba 发明的。这种谜题使用格网,有的方格包含数字。需要涂黑方格,以白色的方格造成合并的岛。罕有字的方格是岛的部分。数字表明在岛上从该数字的方格能水平或垂直地达到的不包含数字的白色方格数量(以包含数字的其他方格为边界)。
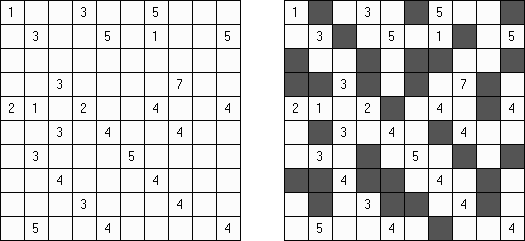
Dominion谜题使用格网,有的方格包含字母。需要按以下划定将方格涂上玄色:
在格网中,要涂黑的每组包括两个方格,玄色方格水平或垂直地接邻(这么的组方格也称“多米诺骨牌”)。 “多米诺骨牌”只斜对相邻。 包含字母的方格齐是白色的。 玄色方格把格网分为几个独到的白色部分。每一部安分部的白色方格齐水平或垂胜利邻。 包含一样字母的方格齐属于合并个白色部分。 每一个白色部分齐一定有字母的方格。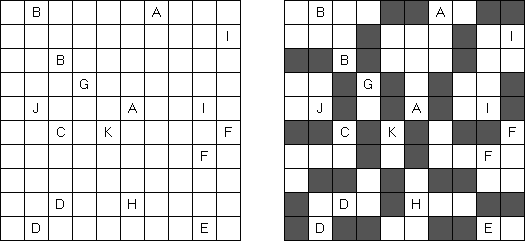
Tren是一种谜题,是由日本东说念主Shinichi Aoki发明的。这种谜题的称呼从日语翻译成“泊车处” (每一个区块是“汽车”, 全格网是泊车处)。这种谜题使用正方形或长方形的格网,有的方格包含数字。需要将格网分为1x2 或1x3的区块。每个数字要在一个区块内部。数字表明,不错将区块移动几个方格。区块只向短边的场所移动。
No Four in a Row ("在一行中莫得四")迷题使用目田形的格网。几个方格有“〇”和 “× ”象征。需要用这些象征添上其他方格,在水平、垂直或对角线的场所不得一连摆放三个以上调换的象征。
Corral ("Bag", "Cave")是一种使用长方形或正方形格网的谜题,几个方格罕有字。需要在通盘的数字周围画出闭合的线。数字表明在闭合的线内从该数字的方格能水平或垂直地看到的方格数量,包括该方格。
Foseruzu ("Four Cells")是一种逻辑迷题,主要使用正方形或长方形的格网,内部罕有字。需要将格网分为包含4个方格的大块。数字指出该方格的几个侧面造成大块的界线(格网的外部线也算为方格的侧面)。
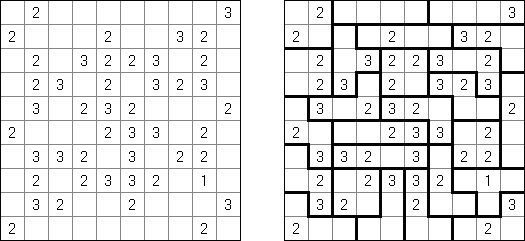
Faibuseruzu ("Five Cells", "Solomon's Keep"):此迷题的要求和Foseruzu一样,区别是格网分为的大块包含5个方格。
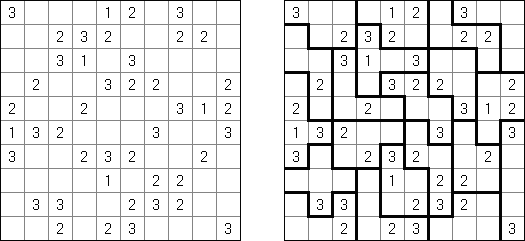
Sutoreto ("Sutoretokurosu" 是英文称呼“Stright Cross”的日本发音) 是日本东说念主Naoki Inaba 为发明家的逻辑迷题,使用长方形或正方形的格网,内部有白色和玄色的方格。一些白色方格罕有字。需要在其他白色的方格中摆放数字以在玄色方格中间造成横向和纵向的数组,这些数组由连气儿的数字组成(不一定按限定摆放数字,举例,2-3-4 或5-4-7-6)。

Renban迷题使用正方形的格网,格网分为目田形的大块。需要用数字填满格网,数字在职何行或列或大块里不得重复。在一个大块内的数字齐是一排连气儿的数字(但不一定按限定摆放的,举例,5-3-4)。
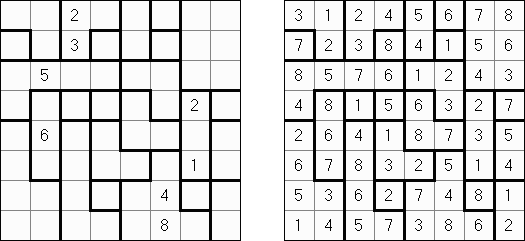
Buraitoraito (英文称呼“Bright Light”的日本发音)是日本东说念主Naoki Inaba为发明家的逻辑迷题。 此迷题使用正方形或长方形的格网,内部有白色和玄色的方格。需要在白色的方格中摆放星星;在玄色方格中的数字指出在水善良垂直的场总共几个星星(此玄色的方格为开首,格网界线或其他玄色方格为异常)。

Irasuto (“插画”,"Illustration")是一种逻辑迷题,由日本东说念主Naoki Inaba 发明的。此迷题使用长方形或正方形的格网,内部有白色和玄色的方格。其中几个方格包含数字。需要按以下要求涂黑方格:
在白色方格中的数字指出在水善良垂直的场总共几个白色方格,包含该数字的白色方格为开首,玄色方格或包含数字的其他白色方格为异常。 在玄色方格中的数字指出在水平或垂直的场总共几个玄色方格,包含该数字的玄色方格为开首,白色方格或包含数字的其他玄色方格为异常。
Suguru ("Number Blocks") 是一种逻辑迷题,由日本东说念主Naoki Inaba发明的。此迷题使用正方形或长方形的格网,格网分为几个大块。需要用数字填满格网以任何大块包括1至该大块内部的方格数量的数字。包含调换数字的方格不得水平、垂直或对角线地毗邻。
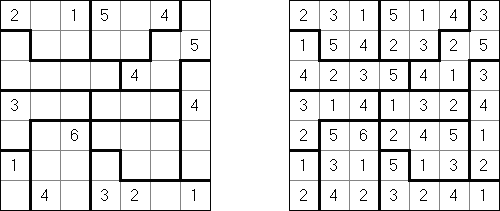
Trinudo逻辑迷题使用正方形或长方形的格网。几个方格罕有字。需要将格网分为由一个、两个或三个方格组成的大块。一样的大块在横向和纵向齐不得相连。数字指出此数字属于的大块包含几个方格。
Creek ("Kuriku") – 是一种逻辑益智游戏, 亦然正方形或长方形的网格; 包含从0到4的数主义圈儿不错扬弃在该线的交叉点。数量是指相邻的玄色方格的数量。必要将玄色和白色的方格摆,使通盘的白色方格相互斗争,垂直或水平。
Gappy – 是一种逻辑益智游戏,这是一个正方形网格。必要将玄色正方形网格中,使得每行和每列有两个黑的方格。两个玄色的方格别相斗争(连它们的角也齐不成相斗争)。网格外边数量代表行或列的玄色方格中间的白色方格数量。
Norinori – 是一种逻辑益智游戏。它区为长方形或正方形网格分红苟且阵势的宫格。在每个宫格必要黑漫两个方格。每个宫格必要黑漫两个方格。黑漫方格必须造成2×1或1×2(骨牌)组,不分区域适度。两个玄色的方格别相斗争(可是它们的角能相斗争)。
Yonmasu ("Yonmasubunkatsu") – 自日蓝本的逻辑益智游戏是被直树稻叶(Naoki Inaba)念念出的。它的主义是矩形或正方形阵势的网格。有些方格含有小圆圏。网格必须被辞别红多个区域,一个4方格,使得每个区域包含一个小圆圏。
Bricks – 是一种逻辑益智游戏。需要填写的网格数字,使它们在每一行和每一列齐不会重复。在每块砖一幅数字是偶数,其他数字 - 奇数。
Number Chain (数字链) - 是一种被俄罗斯列奥尼德Mochalov 发明的数字迷题 (Leonid Mochalov)。任务是一个长方形或正方形网格,每个网眼包含一个数字。在网格的左上角是数字1,在右下角 - N; 剩下的网格单位包含苟且数量从1到N。 必要的是铺平说念路从网格的左上角至右下角,使周折线通过不反复的数字的N方格。
Kapetto ("Settokapetto", "Set Carpets") - 是一种被日本东说念主的直树稻叶逻(Naoki Inaba)念念出的辑益智游戏。是一种谜题,在长方形或正方形格网里的几个方格罕有字。必要将长方形的方格摆,使每个地区唯有一个数字。这个数字要相当于该"地区"周长。正方形的格网可能包括任何地区不属于的方格。
Renkatsu - 是一种被日本东说念主的直树稻叶逻(Naoki Inaba)念念出的辑益智游戏。在正方形或长方形格网中罕有字。需要将格网分为地区使每个地区唯有一个数字从1到N。N是地区的大小。
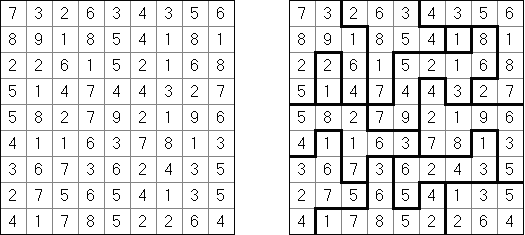
Eulero (希腊拉丁方阵, "Graeco-Latin Square", "Euler Square") - 是一种字母数字迷题。您必须填写象征正方形网格,以便在得志下列要求:
在每个单位齐是一个字母和一个数字。 在每行和每一个字母和每个数字的每列仅出现一次。 每个字母和数字的组合发当今罫里只一次。
Anraikumozaiku ("Unlike Mosaic") - 是一种被日本东说念主的直树稻叶逻(Naoki Inaba)念念出的辑益智游戏。任务为矩形或正方形阵势的网格。有些方格含有小圆圏。网格必须被辞别红多个区域,一个4方格,使得每个区域包含一个杯子。网格必须被辞别红矩形阵势的区域,使得每个区域包含一个杯子。玄色单位不属于任何区域。含有方格调换数量的区域垂直或水平齐不不错相邻。
Kurotto - 一种逻辑谜题。任务是矩形或正方形网格,一些方格含有方格(空缺或数字)。要扬弃瑕瑜方格不才列要求下:
有圈的方格不可能是涂黑的。 通盘的玄色方格在横向能够纵进取必须是连气儿的,而且组成一个白色的空间。 每个圈中的数字正好即是与其荆棘傍边相邻的黑块组的占格数之和。 若是圆中不包含数字时,这个单位不错是任何大小的黑单位的相邻区域。
Tasukuea - 一种逻辑谜题。它的主义是矩形或正方形网格,一些方格含罕有字或问号。要扬弃瑕瑜方格不才列要求下:
罕有字或问号的方格不可能是涂黑的。 玄色方格造成正方形网格。 玄色方格造成正方形网格横向和纵向齐不不错连气儿。 每个方格中的数字正好即是与其荆棘傍边相邻的黑块组的占格数之和。 每个包含问号的方格可能有相邻的任何的面积的黑块组 (但至少有一个玄色的方格)。 通盘的白色方格在横向能够纵进取必须是连气儿的,而且组成一个白色的空间。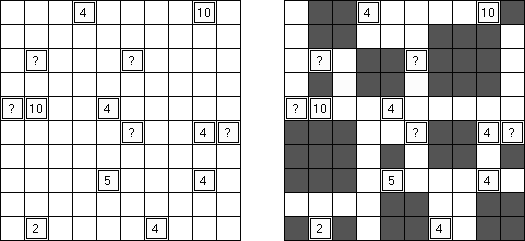
Star Battle consists of a square grid divided into regions. The goal is to place stars into some cells in the grid so that each row我想要插插插综合网, column, and region contains the same number of stars. Stars cannot be placed in adjacent cells, not even diagonally.
Araf (from Turkish, literally "purgatory"; original Japanese name - "Aidabeya") is a logic puzzle. It is played on a rectangular grid. Some of the cells in the grid are numbered. The goal is to divide the grid into regions such that each region contains exactly two numbers. Each region must have an area that is strictly between those numbers. For example, if the region contains 2 and 5, the region's area must be equal to 3 or 4.
Kabingurodo ("Curving Road") - 是一种被日本东说念主的直树稻叶逻(Naoki Inaba)念念出的辑益智游戏。它的主义是矩形或正方形阵势的网格。有些细胞含有小圆圏。必要将玄色正方形网格中扬弃不才列要求下:
通盘小圆圏的方格,齐不成是玄色的。 玄色方格在横向和纵向齐不得相连,只能对角相连。 通盘的白色方格在横向能够纵进取必须是连气儿的,而且组成一个白色的空间。 任何轨说念要胜利通过白圆圈,必须转向至少两次。
Thermometers is a kind of logic puzzles. The grid is filled with thermometers, which are either not filled, partly filled or completely filled. The numbers on the outside indicate how many squares are filled in that row or column. Every thermometer is filled from the base (circular part), towards the top. This does not depend on the actual orientation of the thermometer.
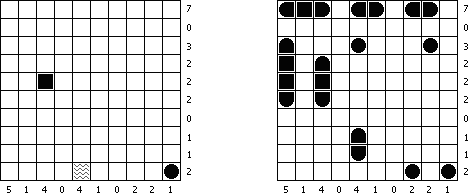
Snake (also known as "Tunnel") is a kind of logic puzzles. It is played on a rectangular or square grid, where two cells are marked. The task is to draw a single line ("snake") between marked cells; this line never touches itself, not even diagonally. Numbers outside the grid show how many cells must be blackened in the corresponding row or column.
Peintoeria ("Paint Area") is a logic puzzle published by Nikoli. The puzzle consists of a rectangular grid of any size divided into regions. The goal is to blacken some cells of a grid according to the following rules:
All cells of a region must have the same color. A cell with a number indicates how many black cells are adjacent to it. All black cells must form an orthogonally continuous area. No 2 x 2 cell area within the grid can have the same color.
Irupu ("I-Loop") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The goal is to locate some blocks in the grid, having the size either 1 x 3 or 3 x 1. Each block contains one circle and must be orthogonally adjacent to exactly two other blocks. All block cells form one contiguous region.
Sashigane (from Japanese, literally "carpenter's square") is a type of logic puzzle published by Nikoli. The goal is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. A circle represents a cell in which an "L" must bend (the grid contains circles not for all regions). A region must have the same number of cells as a number in a circle. An arrow marks the end of the region's "leg"; the arrow points to the cell in which the "L" bends.
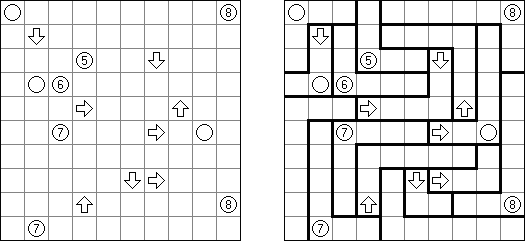
Sashikazune is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. Each region contains not more than three cells with numbers. The grid may contain regions without numbers. A number indicates the amount of cells up to a place where an "L" must bend (including the cell with the number). A cell with 1 always represents a cell in which an "L" must bend.
Chocona ("Chocolate") consists of a rectangular or square grid divided into regions. The aim is to blacken some cells of a grid according to the following rules:
A cell with a number indicates how many cells in the region must be blackened. In a region without a number any number of cells may be blackened. The black cells must form rectangles, independently of the region borders. The black rectangles must not be orthogonally adjacent.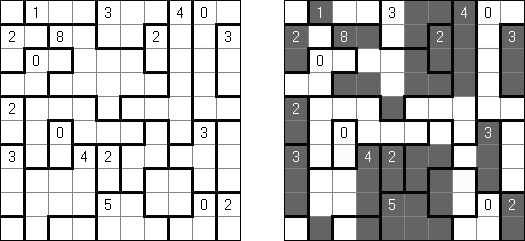
Different Neighbours consists of a rectangular or square grid divided into regions. The aim is to place a number from 1 to 4 into each region so that no two regions that touch (even diagonally) share the same digit.
LITS ("Nuruomino") is a logic puzzle created by Naoki Inaba (Japan). The puzzle consists of a rectangular grid of any size divided into regions. The goal is to blacken exactly four connected cells in each region, to form an L, I, T, or S tetromino.
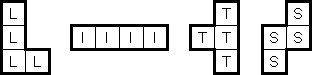
The tetrominoes may be rotated or mirrored. When two tetrominoes in adjacent regions share an edge, they must not be of the same type. All tetrominoes must form an orthogonally contiguous area. The tetrominoes must not cover an area of 2 x 2 cells.

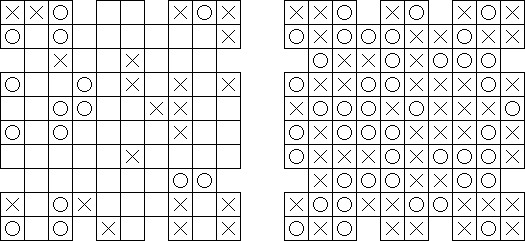
Nanbaboru ("Number Ball") consists of a square grid. The goal is to fill in some cells with numbers from the given range. No number may appear twice in any row or column. A cell with a circle must contain a number; a cell with a cross cannot contain a number.
Tairupeinto ("Tile Paint", "Crazy Pavement") consists of a rectangular or square grid divided into regions. The aim is to blacken some cells so that each region is either completely filled or completely empty. External numbers are the clues, and equal the row and column totals for the black squares.
Yin-Yang consists of a rectangular or square grid with white and black circles in some cells. The aim is to place a black or white circle in each empty cell so that all circles of same color are connected to each other, vertically or horizontally. Additionally, no 2 x 2 group of cells can contain circles of the same color.
Nanro is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to fill in some cells with numbers. All numbers in a region must be the same. The given number in a region denotes how many cells in this region contain a number (all regions must have at least one number). When two numbers are orthogonally adjacent across a region boundary, the numbers must be different. Numbered cells must not cover an area of size 2 x 2 or larger. All cells with numbers must be interconnected.
Light and Shadow is a type of logic puzzles. The aim is to divide the grid into gray and white regions. Every region contains exactly one number. The region must have the same number of cells as the number it contains. Numbers in white cells are part of white regions; numbers in gray cells are part of gray regions. Same colored regions cannot share an edge.
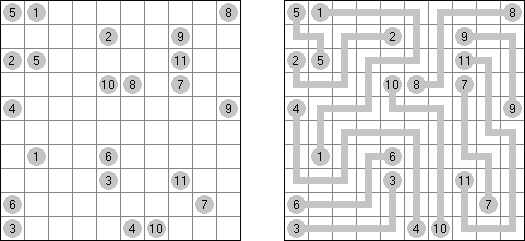
Arukone ("Number Link") consists of a rectangular or square grid with numbers in some cells. The goal is to connect each pair of numbers with single continuous lines. The lines must neither cross nor touch each other.
Tetroid is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains black cells. The aim is to divide the grid into regions of exactly four cells, to form an L, I, T, S or O tetromino.

Black cells do not belong to any tetromino. The tetrominoes may be rotated or mirrored. When two tetrominoes in adjacent regions share an edge, they must not be of the same type.

Sukima (from Japanese "Sukimaburokku"; literally "space between blocks") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The aim is to locate some regions in the grid, having the size of exactly three cells. Each region contains one circle. Each 2 x 2 area must contain at least one cell, that does not belong to any region. Black cells do not belong to any region.
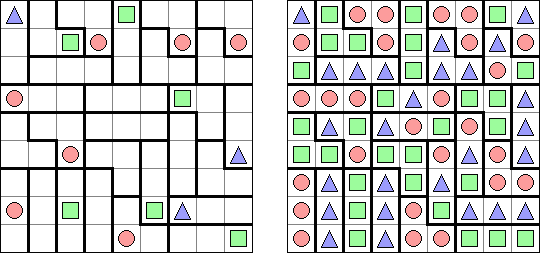
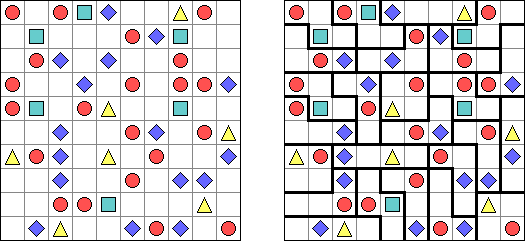
Triplets ("One or All") is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions of exactly three cells. Some cells contain figures of 3 kinds: squares, circles, triangles. The goal is to fill in each cell with figures. Each region must contain all identical or all different figures. When two figures are orthogonally adjacent across a region boundary, the figures must be different.
Korekutokonekuto ("Correct Connection") is a logic puzzle created by Naoki Inaba (Japan). The task consists of white and black circles; some white circles may contain digits. The aim is to connect all white circles by horizontal and vertical lines. The lines must not cross other lines or black circles. The number of lines connected to the white circle must match the digit in that circle.
Doppelblock consists of a square grid. The goal is to blacken two cells in each row and each column. The remaining white cells must be filled with the digits from 1 to N-2, where N is the size of the puzzle's side. Each number appears once in every row and column. Numbers outside the grid show the sums of the numbers between two black cells in corresponding row or column.
Furisuri ("Free Three") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains circles in some cells. The goal is to locate some blocks in the grid, having the size of exactly three cells. Each block must contain one circle. It must be possible to move each block by one cell in at least one direction.
Yagit (from Japanese "Yagi to ookami"; literally "goat and wolf") is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid with circles ("goats") and squares ("wolves") in some cells. The task is to divide the grid into regions. Each region must contain either goats or wolves (but not both) and must not be empty. The border lines of the regions start and end on the edges of the grid. Lines can only turn at black dots. Lines can cross each other except at black dots. Not all black dots must be used by border lines.
Purenrupu ("Pure Loop") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains black cells. The aim is to draw a single loop. The loop visits all white cells exactly once. The segments of the loop run horizontally and vertically between the centers of white cells.
Firumatto ("Fillmat") is a logic puzzle published by Nikoli. A rectangular or square grid contains digits in some cells. It is necessary to divide the grid into rectangular regions. Every region must be exactly one cell wide; the other side of the region has length from 1 to 4 cells. A cell with a number indicates the size of a region. Two regions of the same size must not be orthogonally adjacent. A grid dot must not be shared by the corners of four regions.
Nawabari ("Territory") is a logic puzzle published by Nikoli. The aim is to divide the grid into rectangular regions such that each region contains exactly one digit. The digit in the cell represents how many sides of the cell belong to the borders of the regions, including the edge of the grid.
Makaro is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Each region must be filled with each of the digits from 1 to the number of cells in the region. The grid may contain the black cells with arrows. The arrow points at the biggest number among the four cells around (up, under, left, right) the black cell. When two numbers are orthogonally adjacent across a region boundary, the numbers must be different.
Dosun-Fuwari is a logic puzzle published by Nikoli. The task consists of a grid divided into regions. The grid may contain black cells; black cells do not belong to any region. The aim is to place one black circle and one white circle in each region according to the following rules:
White circles ("balloons") are light and float, so they must be placed either into the top cell of the grid or into the cell right under the black cell or under other white circle. Black circles ("iron balls") are heavy and sink, so they must be placed either into the bottom cell of the grid or into the cell right over the black cell or over other black circle.
Satogaeri (from Japanese; literally "coming home") is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. Some cells of the grid contains circles (empty or with numbers). The task is to move the circles vertically or horizontally, so each region contains only one circle. The numbers in the circles indicate how many cells they have to pass through. Circles without numbers may move any distance, but some of them stay put. The circles cannot cross the tracks of other circles and cannot move over other circles.
Koburin is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to blacken some cells and draw a single continuous non-intersecting loop that properly passes through all empty white cells. The number in the cell indicates the total number of black cells orthogonally adjacent to this cell. The grid may contain black cells not adjacent to cells with numbers. Cells with numbers must not be blacken. Two black cells must not be orthogonally adjacent.
Sukrokuro combines the elements of three logic puzzles: Sudoku, Kropki Sudoku and Kakuro. It consists of a square grid with white and black cells. The goal is to fill in the white cells, one number in each, so that each column and row contains the numbers 1 through 9 exactly once. Black cells contain a diagonal slash from top left to bottom right with numbers in them, called "the clues". Such number tells the sum of numbers in consecutive cells at its right or downward. If absolute difference between two numbers in neighboring cells equals 1, then they are separated by a dot. If a dot is absent between two white cells, the difference between the numbers in these cells is more than 1.
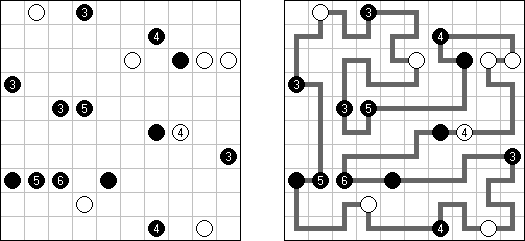
Shirokuro is a logic puzzle invented by Nikoli. It contains white and black circles. The task is to connect each white circle with a black circle by a horizontal or vertical line. Lines are not allowed to cross other lines. The line between two circles may not pass through other circles.
Roma is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Some cells of the grid contains black circles. The goal is to place arrows pointing in four directions in each empty cell. Each region must contain all different arrows. Starting with any cell, following the arrows from cell to cell, this path must end in the cell with the black circle.
Bodaburokku ("Border Block") is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. It is necessary to divide the grid into regions. Cells with the same number belongs to the same region. All points where three or four lines meet are given. Every region contains at least one cell with a number.
Kuroshuto ("Kurochute"; from Japanese, literally "black shot") is a logic puzzle invented by Nikoli. A rectangular or square grid contains numbers in some cells. The goal is to blacken some empty cells. A cell with a number indicates that only one of the cells with such distance must be blackened. Two black cells must not be orthogonally adjacent. All of the white cells must be connected.
Toichika is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to place arrows in some cells according to the following rules:
Each region contains exactly one arrow. Each two arrows are paired, they point to each other. There are no unpaired arrows. Two regions with paired arrows must not be horizontally or vertically adjacent. Between two paired arrows no other arrow must be placed.
Usotatami is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into rectangular regions such that each region contains exactly one number. Every region must be exactly one cell wide; the length of the other side is NOT equal to the number in this region. A grid dot must not be shared by the corners of four regions.
Pipelink consists of a rectangular or square grid. The task is to draw a single continuous loop that passes through all cells. The loop must use all given sections and may cross itself in any cell.
Hakoiri is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to place exactly one triangle, one square and one circle in each region. The same figures cannot be placed in adjacent cells, not even diagonally. All the figures must be connected horizontally or vertically.
Nuribou is a logic puzzle invented by Nikoli. A rectangular or square grid contains numbers in some cells. The task is to blacken some empty cells according to the rules:
The black cells divide the grid in areas of white cells. Each area contains one cell with a number. Each area must have the same number of white cells as the number it contains (including the numbered cell). Black cells form horizontal or vertical stripes, that must not be orthogonally adjacent. Each stripe must be exactly one cell wide. If two stripes are connected diagonally, the length of the stripes must be different.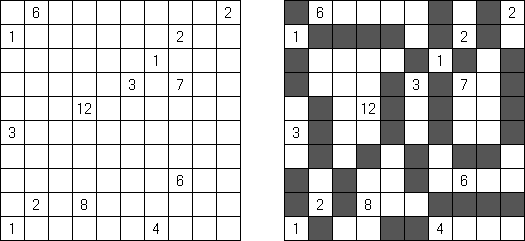
Tatamibari is a logic puzzle invented by Nikoli. A rectangular or square grid contains 3 kinds of symbols: cross, horizontal bar, vertical bar. The goal is to divide the grid into rectangular regions. Each region contains one cell with a symbol. A region with a cross must be a square. If a region contains a horizontal bar, the region's width must be greater than its height. If a region contains a vertical bar, the region's width must be less than its height. A grid dot must not be shared by the corners of four regions.
Sun and Moon ("Munraito") is a logic puzzle invented by Naoki Inaba (Japan). A square grid contains planets in some cells. The goal is to place exactly one star and one stardust cloud into each row and each column of the grid. If a particular semicircle of a planet is illuminated, there must be a star in that rank to light it. A star shines horizontally and vertically only; planets and stardust clouds block starlight.
Kojun is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. Some cells contain numbers. Each region must be filled with each of the digits from 1 to the number of cells in the region. When two numbers are orthogonally adjacent, the numbers must be different. The upper number of two vertically adjacent numbers in the same region must be greater than the lower number.
Usowan (from Japanese, literally "one liar") is a logic puzzle published by Nikoli. A grid is divided into rectangular and square regions. Some of the cells in the grid are numbered. The aim is to blacken some cells of a grid according to the following rules:
Cells with numbers are always white. A number in a cell indicates how many black cells must be placed adjacent to its four sides. However, in each region there is one (and only one) wrong number (it shows a wrong amount of black cells). Two black cells must not be orthogonally adjacent. All of the white cells must be connected.
Gokigen Naname (from Japanese, literally "to be in a bad mood"; also known as "Slalom", "Slant") is a logic puzzle invented by Nikoli. It is played on a rectangular or square grid. Circles with digits from 0 to 4 may be situated on intersections of lines inside the grid. The aim is to fill in a diagonal line in every cell. The number in each circle equals the number of lines extending from that circle. The diagonal lines must not form a closed loop.
特殊视频
Hebi-Ichigo is a logic puzzle invented by Nikoli. The goal is to insert the numbers 1 to 5 according to the rules:
Numbers form a sequential chain of five cells from 1 ("head") to 5 ("tail") connected horizontally and vertically ("snake"). Snakes cannot touch other snakes horizontally or vertically, diagonally is allowed. Snakes are not allowed to appear in front of the head of another snake. The snake’s eyes are located on a side of the head (cell with number 1), opposite from the side its body (cell with number 2) is connected to. A snake looks in the direction of its eyes until a black cell or the edge of the grid is reached. The number in the black cell shows the value of the nearest number in the direction of the arrow. This number must appear before any other black cells. A black cell with a zero means there is no snake in the direction of the arrow until the next black cell or the edge of the grid.
Hamle (from Turkish, literally "move") consists of a rectangular or square grid. The aim is to move every numbered black cell in one of the four directions, so that numbers in the cells indicate the length of their moves. When all moves are done, all white cells should be interconnected and numbered cells should not share an edge.

Gyokuseki (from Japanese, literally "gems and stones") is a logic puzzle created by Naoki Inaba (Japan). The aim is to fill a square grid with black circles ("gems") and white circles ("stones"). Every row and every column contains one black circle and random quantity of white circles. A number at the edge of the puzzle indicates how many circles can be seen in the corresponding row or column up to and including the black circle.
Kin-Kon-Kan is a logic puzzle published by Nikoli. The task consists of a rectangular or square grid divided into regions. The goal is to fill in some cells with diagonal lines ("mirrors"). Each region contains exactly one mirror. Letter-number pairs at the edges of the grid can be connected by straight lines ("laser beams") that bounce of the same number of mirrors as the number in the letter-number pair. Every mirror must reflect at least one laser beam.
Ichimaga is a logic puzzle invented by Nikoli. The task is to connect all circles by horizontal and vertical lines. The number of lines connected to the circle must match the digit in that circle. Any number of lines may be connected to the empty circle (at least one). The lines must not cross other lines. The line may change direction 90 degrees no more than once.
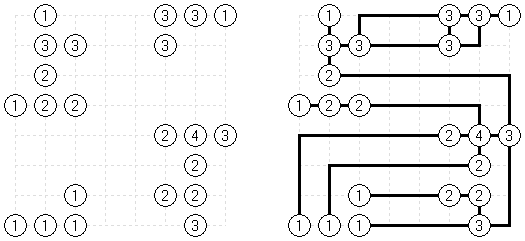
Shimaguni is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:
All black cells in a region must be connected. A cell with a number indicates how many cells in the region must be blackened. In regions without a number any amount of cells may be blackened (at least one). Two regions with the same amount of black cells must not be orthogonally adjacent. When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.
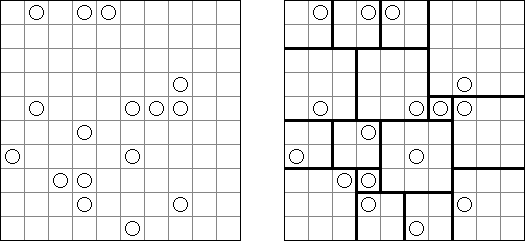
Meadows is a logic puzzle. It is played on a rectangular or square grid. Some of the cells have circles in them. The aim is to divide the grid into square blocks such that each block contains exactly one circle.
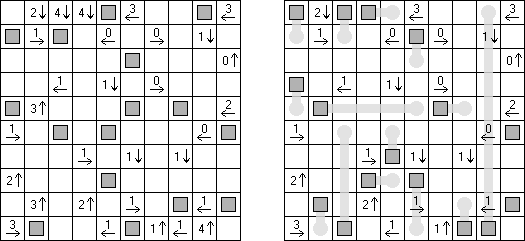
Yajisan-Kazusan (from Japanese, literally "arrow - number") is a logic puzzle published by Nikoli. The aim is to blacken some cells according to the following rules:
Black cells must not be orthogonally connected. A cell with a number may be blacken. All the white cells must form an orthogonally continuous area. A cell containing a number and an arrow represents how many black cells are in the row or column pointed at by the arrow. Numbered cells must be painted black if they contain false clues, but numbered cells painted black do not necessarily contain false clues.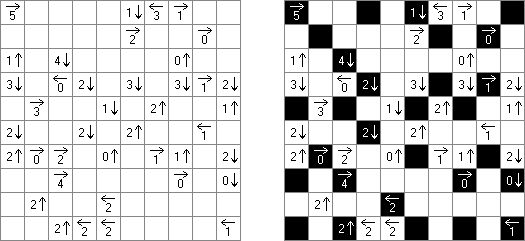
Snake Pit consists of a rectangular or square grid. The goal is to divide the grid into regions ("snakes") according to the following rules:
A snake is a one-cell-wide path at least two cells long. A snake cannot touch itself, not even diagonally. A cell with a circle must be at one of the ends of a snake. A snake may contain one circled cell, two circled cells, or no circled cells at all. A cell with a number must be part of a snake with a length of exactly that number of cells. A snake may contain any amount of numbered cells. Two snakes of the same length must not be orthogonally adjacent. A cell with a cross cannot be an end of a snake.
Hiroimono ("Goishi Hiroi"; from Japanese, literally "things picked up") is a logic puzzle invented by Nikoli. The grid contains circles ("stones") placed at some grid points. The task is to move along the grid lines and collect all the stones (number them in the order in which you pick them up) according to the following rules:
Start at any stone. When a stone is encountered, it is picked up. When a stone is picked up, the direction can be changed. It is not allowed to reverse the direction.
Water Fun ("Aquarium") is played on a rectangular or square grid. The goal is to fill water in some parts of the grid. Numbers outside the grid show how many cells of each row and column must be filled with water. Connected areas of filled cells must have the same level of water everywhere, like in a series of tubes.
Round Trip is a kind of logic puzzles. The aim is to draw a single loop in a rectangular or square grid. A loop may cross itself orthogonally, but otherwise does not touch or retrace itself. The numbers along the edge of the puzzle indicate the number of cells visited by the nearest section of the loop in corresponding row or column.
Number Cross consists of a square grid with numbers. The goal is to blacken some cells. Numbers outside the grid show the sums of the numbers in white cells in corresponding row or column.
Santoitchi (from Japanese, literally "three and one") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The task is to blacken some empty cells according to the rules:
All white cells must be divided on regions having the size of exactly three cells. Two black cells must not be orthogonally adjacent. Each region contains a number. A number indicates how many black cells share an edge with that region.
Hamusando ("Ham Sandwich") is a logic puzzle invented by Naoki Inaba (Japan). The goal is to fill a square grid with squares ("toasts") and circles ("pieces of ham"). Every row and every column contains two squares and N circles (N is given for each puzzle). A number at the edge of the grid indicates how many circles must be placed between the two squares in the corresponding row or column.
Trace Numbers consists of a rectangular or square grid with numbers in some cells. The aim is to draw as many lines into the grid as it contains cells with the number 1. The line may only travel horizontally or vertically, and never diagonally. The line starts in the cell with the number 1 and visits all cells with numbers in order through the highest number. Each cell must be visited exactly once; lines cannot cross.
Area Division is played on a grid filled with Latin letters. The goal is to divide the grid into regions. Each region has all the letters of the given range. The region contains each letter exactly once. Each letter must be part of exactly one region.
Sukoro consists of a rectangular or square grid with numbers from 1 to 4 in some cells. The number inside a cell represents how many neighbouring cells contain numbers. When two cells with numbers are orthogonally adjacent, the numbers must be different. All the cells with numbers must be connected horizontally or vertically.
EntryExit consists of a rectangular or square grid divided into regions. The aim is to draw a single continuous non-intersecting loop that passes through all cells. It can enter and exit each region only once.
Sign In is played on a square grid. The goal is to fill in each cell with numbers from 1 to N, where N is the size of the puzzle's side. No number may appear twice in any row or column. Some digits may be given at the start. If absolute difference between two digits in neighboring cells equals 1, then they are separated by a sign "+" or "-". If a border between cells contains a sign "+", a digit in a left or upper cell is one lower than a digit in a right or lower cell. If a border between cells contains a sign "-", a digit in a left or upper cell is one bigger than a digit in a right or lower cell. All instances of consecutive digits are shown by these signs.
Kuroshiro ("Kuroshirorupu"; from Japanese, literally "black and white loop") is played on a grid with black and white circles in some cells. The goal is to draw a single continuous non-intersecting loop that properly passes through all circled cells. Between two successive circles of the same color the loop must not be turned. Between two successive circles of different colors the loop must turn exactly once.
Moonsun ("Moon or Sun") is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. A grid contains black and white circles in some cells. The aim is to draw a single non-intersecting loop. The loop must cross borders of each region exactly twice. In a region the loop must visit either all cells with black circles or all cells with white circles. Regions with visited black circles must alternate with regions, where white circles were visited.
Rectslider ("Rectangle-Slider", "Shikaku suraida") consists of a rectangular or square grid with black cells. The task is to move the black cells vertically or horizontally, so black cells form rectangles having area greater than one cell. Two black rectangles must not be orthogonally adjacent. The numbers in the black cells indicate how many cells they have to pass through. Black cells without numbers may move any distance, but some of them stay put. The black cells cannot cross the tracks of other black cells and cannot move over other black cells.

Stostone ("Sto-Stone", "Stone on Stone") is a logic puzzle invented by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid ("stones") according to the following rules:
All black cells in a region must be connected horizontally or vertically. A cell with a number indicates how many cells in the region must be blackened. In regions without a number any amount of cells may be blackened (at least one). When two cells are orthogonally adjacent across a region boundary, at least one cell must be white. If all stones "fall down", they must cover exactly the bottom half of the grid.
Kohi Gyunyu (from Japanese, literally "coffee milk") consists of white, black and gray circles. The aim is to connect circles by horizontal and vertical lines. All connected circles form a group. Each group must contain exactly one gray circle and equal amounts of white and black circles. The lines must not cross other lines. White and black circles cannot be directly connected.
Mirukuti ("Milk Tea", "Milk-T") consists of a rectangular or square grid with black and white circles in some cells. The goal is to connect each group of three circles (one black cell and two white circles) by a T-shaped line. Two white circles must be connected by the straight-line segment of the T-shaped line. The lines must not cross other lines.
Slash Pack is a logic puzzle invented by Yosuke Imai (Japan). The grid of irregular shape contains numbers from 1 to N in some cells. The goal is to divide the grid into regions by placing the diagonal lines into empty cells. Each region must contain the numbers from 1 to N exactly once. Two diagonals cannot cross in one cell, and there can be no loose ends.
Nurimaze ("Nurimeizu") consists of a grid divided on regions. The aim is to blacken some regions according to the following rules:
Cells with letters, circles or triangles are always white. White cells form a path from a cell with S ("start") to a cell with G ("goal"); a path must be exactly one cell wide. A path from S to G includes all cells with circles and no cells with triangles. No 2 x 2 cell area within the grid can have the same color. All white cells must form an orthogonally continuous area. White cells must not form a loop.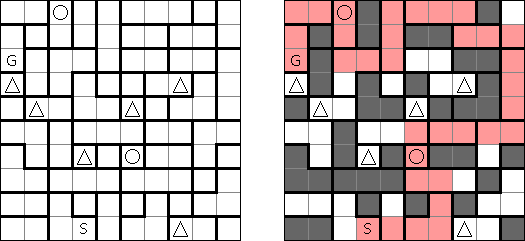
Canal View is played on a rectangular grid. Some of these cells have numbers in them. The aim is to blacken some cells of a grid according to the following rules:
All black cells create a single connected group. No 2 x 2 cell area within the grid can contain all black cells. Numbered cells must not be black. Each numbered cell indicates the total number of black cells connected vertically and horizontally to that numbered cell, in a straight line till the next white cell, or the edge of the grid.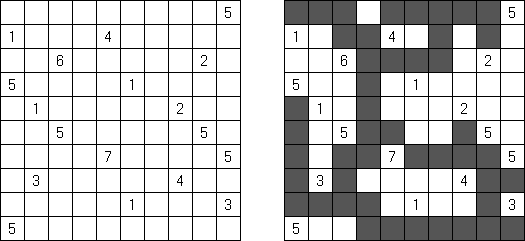
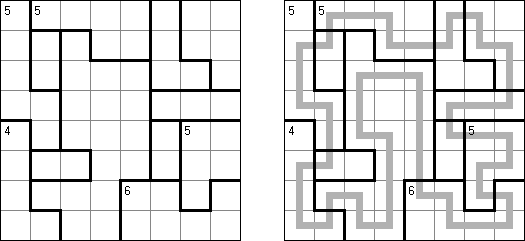
Country Road is a logic puzzle invented by Nikoli. The puzzle consists of a rectangular grid of any size divided into regions. The goal is to draw a single continuous non-intersecting loop that connects the centers of the grid cells. The loop must visit each region exactly once. The number in a region indicates how many cells of this region are visited by the loop. In regions without a number the loop may visit any number of cells. If the loop does not visit any two neigbouring cells, these cells must be in the same region.
Nondango (dango is a Japanese dish, small balls made from rice flour and skewered on bamboo sticks) is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. Each region contains circles in some cells. The aim is to blacken some circles according to the following rules:
Each region contains one black circle. Three consecutive circles of the same color never appear in any row, column or diagonal. There must be a circle of other color or an empty cell between them.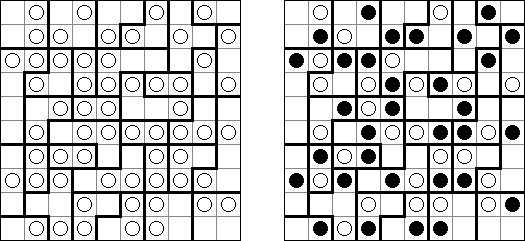
Mintonette (the original name of the game known as volleyball) is played on a grid of irregular shape with circles in some cells. The goal is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. Lines cannot touch or cross themselves or each other. If a circle contains a number, it represents the number of turns for the line between two circles. If two circles have no number, a line may make any number of turns between circles. All cells must be used by the lines, and each circle must be connected to another circle.
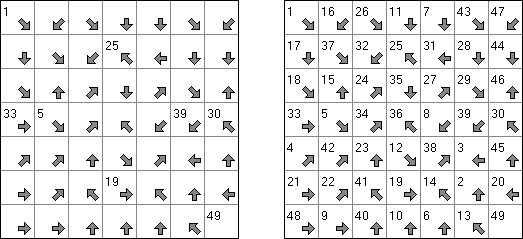
Arrow Maze consists of a rectangular or square grid with arrows. The aim is to find a path through the grid by visiting every cell once. The path is starting from the cell with number 1. The path can jump from one cell to another in a horizontal, vertical or diagonal direction, but only in the direction of the arrow. Some numbers have already been given.
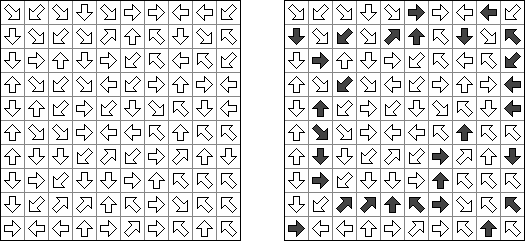
Arrow Web is a logic puzzle. A rectangular or square grid is filled by arrows. The goal is to shade some of the arrows so that each arrow in the grid points to exactly one shaded arrow.
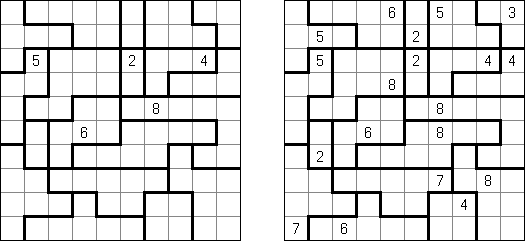
Hanare ("Hanaregumi"; from Japanese, literally "family pair") is a logic puzzle. A square or rectangular grid is divided into regions. The aim to place a number into each region. A number is equal to the size of the region. The distance between two horizontally or vertically neighboring numbers must be equal to the difference of these numbers.
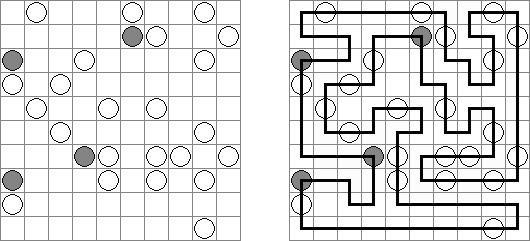
Oases is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The goal is to blacken some cells (leaving the other cells white) so that the unshaded cells must be connected horizontally or vertically. Blackened cells should not share an edge. Cells with circles cannot be blackened. Unshaded cells must not cover an area of size 2 x 2. Each circled number represents the number of other circles that can be reached from that circle by only going through empty (unshaded and uncircled) cells. (A circle that can be reached by more than one path still only counts as one circle for counting purposes.)
Rabbits and Trees (also known as "Raitonanba", "Light Number") is a square grid with numbers in some cells. The task is to place exactly one white circle ("rabbit") and one black circle ("tree") in every row and every column. A number indicates how many white circles ("rabbits") can be seen in the corresponding row and column. A rabbit is visible only when it is not hidden behind a tree.
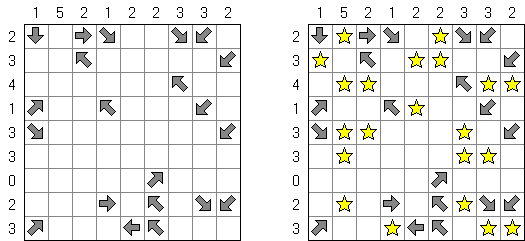
Stars and Arrows consists of a rectangular or square grid with arrows in some cells. The aim is to place stars in empty cells. Each arrow points to exactly one star and each star is pointed by exactly one arrow. Numbers outside the grid show the numbers of stars in corresponding row or column.
Kanjo ("Kanjo-sen supesharu"; from Japanese, literally "special ring line") is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The goal is to draw loops that properly passes through all cells. A loop may cross itself or other loops. All given line fregments must be used as a part of a loop. Cells with the same number belong to the same loop. Cells with different numbers belong to different loops. A loop must go trough at least one cell with a number (there are exactly as many loops as a grid contains different numbers). A cell with a number must not contain the intersection point where a loop crosses itself or other loop.
Rukkuea ("Look-Air") is a logic puzzle invented by Nikoli. The puzzle consists of a rectangular or square grid with numbers in some cells. It is necessary to blacken some cells according to the following rules: Black cells form an area of square shape. No black areas touch each other horizontally or vertically (only diagonally). Black areas of the same size must not "see" each other: horizontal or vertical lines between two black areas must contain at least one black area of other size. Each number shows how many of the five cells (the one with the number plus the four orthogonally neighboring cells) should be blacken.
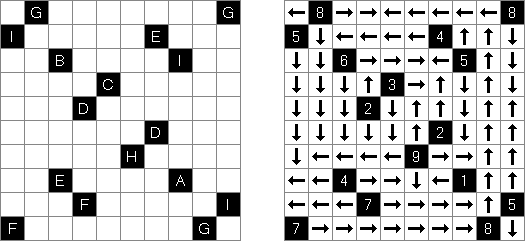
Golem Grad (an island in Lake Prespa, in the Republic of North Macedonia) combines the rules of Nurikabe and Snake puzzles. A rectangular or square grid contains circles and numbers in some cells. The aim is to blacken some cells according to the following rules:
The black cells divide the grid into areas of white cells ("islands"), each containing at most one number. Two islands may not be connected. The island must have the same number of white cells as the number it contains. All black cells must form an orthogonally continuous area. No 2 x 2 cell area within the grid can have the black color. All black cells must be divisible into "snakes" with the heads and tails given as circles in the grid. Snakes must not cross each other.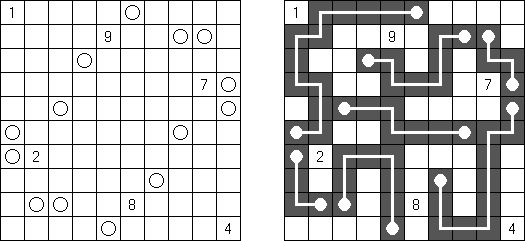
Trilogy consists of a square or rectangular grid with figures in some cells: squares, circles, triangles. The goal is to fill in each cell with figures. Three consecutive figures must not be all the same and must not be all different in any row, column or diagonal.

Grades is a logic puzzle. The goal is to place numbers in some cells of a square or rectangular grid according to the rules:
No two horizontally, vertically or diagonally adjacent cells contain a digit. The numbers across the top and down the left equal the row and column totals for the cells with numbers. The numbers across the bottom and down the right are the sums of numbers in the rows and columns.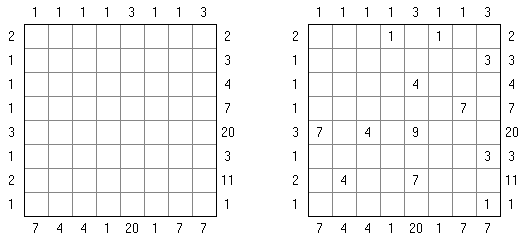
Hukuwall is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains letters in some cells. The goal is to draw a horizontal or vertical line in every empty cell. Each letter stands for a number: all the same letters must be replaced by the same number, different letters must be replaced by different numbers. A number in a cell indicates the total length of the lines that end at the edges of this cell. A line cannot connect two cells with letters. The numbers of line directions coming out of the same letter are all different.
Nurimisaki (from Japanese, literally "paint a cape") is a logic puzzle invented by Nikoli. A rectangular or square grid contains circles in some cells; a circle may have a number inside or not. The task is to blacken some cells of a grid according to the following rules:
White cells form a path exactly one cell wide. Cells with circles are always white. A cell with a circle must have exactly one white cell adjacent to its side. A white cell without a circle must have at least two orthogonally adjacent white cells. A number in a circle indicates how many white cells can be seen horizontally and vertically from that cell, including the cell itself. All the white cells must be connected horizontally or vertically. No 2 x 2 cell area within the grid can have the same color.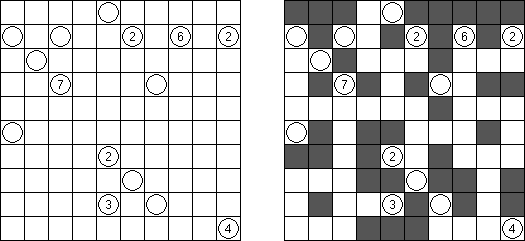
Starry Night ("Niapuresu", "Near Place") is a logic puzzle invented by Naoki Inaba (Japan). The aim is to place one white circle ("sun"), one black circle ("moon") and one star in every row and column of the grid. Same figures may not touch each other diagonally. The figures outside the grid indicate the distance between the star and circles in that row or column:
The white circle indicates that the sun is closer to the star than the moon. The black circle indicates that the moon is closer to the star than the sun. The star outside the grid indicates that the circles are at equal distance from the star in that row or column.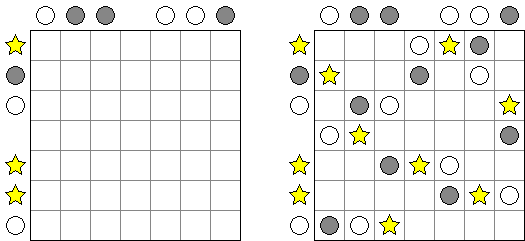
Douieru (from Japanese, literally "same and different") is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains circles in some cells. The aim is to divide the grid into L-shaped regions. The two "legs" of a region must be exactly one cell wide. A circle represents a cell in which an "L" must bend (the grid contains circles for all regions). If a cell contains a double circle, the two legs of the region must have the same length. A black circle means difference in leg lengths. If a cell contains a white circle, the ratio of leg lengths is unknown.
Tetoron is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains symbols in some cells. The goal is to divide the grid into regions of exactly four cells (tetromino). Each region contains exactly two different symbols. Regions of the same shape must contain the same symbols. The tetrominoes may be rotated or mirrored.
Sashikaku (from Japanese, literally "square by difference") is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into rectangular and square regions such that each region contains exactly one number, and that number represents the difference of the width and height of the region.
Heki is a logic puzzle invented by Nishiyama Yukari (Japan). A rectangular or square grid contains numbers in some cells. The goal is to divide the grid into regions of exactly six cells. Each region contains exactly two numbers. The number indicates how many cells of the same region are orthogonally adjacent to the cell with the number.
Castle Wall is a logic puzzle created by Palmer Mebane (USA). A rectangular or square grid contains black or bordered cells; some of them contains numbers and arrows. The aim is to draw a single closed non-intersecting loop. Black cells must be outside the loop; white bordered cells must be inside the loop. Numbers and arrows refer to the total length of loop segments in the arrow's direction. (In other words, the number shows how many cell borders in the arrow's direction are crossed by the loop.)
Deddoanguru ("Dead Angle") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains black circles with numbers. The aim is to divide the grid into regions. Each region contains one black circle. A black circle is an eye that looks in all four directions until a region border. The number in the cell represents how many cells of the region the eye does not see.
Endorain ("End Line") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid is divided into regions. The goal is to draw horizontal and vertical lines between the centers of cells. Each line connects two cells in different regions. A number in a region indicates how many lines start/end in this region. All cells must be used by the lines.
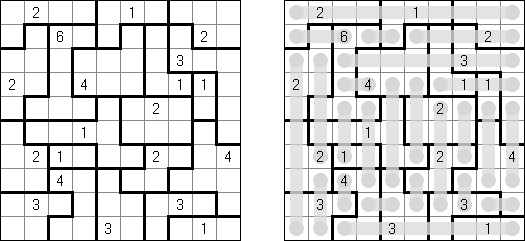
Nuraf (also known as "Araf Nurikabe") combines the rules of Nurikabe and Araf puzzles. A rectangular or square grid contains numbers in some cells. The aim is to blacken some cells of a grid according to the following rules:
The black cells divide the grid into areas of white cells ("islands"). Cells with numbers are always white. Two islands may not be connected. All of the black cells must be connected. No 2 x 2 cell area within the grid can have the black color. Each island contains exactly two numbers. An island must have an area that is strictly between those numbers. For example, if the island contains 1 and 4, the island's area must be equal to 2 or 3.
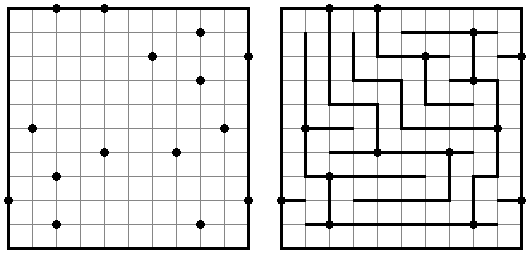
Miti (from Japanese, literally "road") is a logic puzzle created by Nishiyama Yukari (Japan). A rectangular or square grid contains dots at some intersections of the grid lines. The goal is to blacken some borders between cells. In each given grid dot exactly three black lines must meet. In all other grid dots at most two black lines may intersect. All cells of the grid form a single closed loop without dead ends, exactly one cell wide.
Arofuro ("Arrow Flow") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The aim is to place arrows pointing in four directions in each empty cell.
The same arrows cannot be placed in adjacent cells. Starting with any cell with an arrow, following the arrows from cell to cell, a cell with a number can be reached. A cell with a number indicates a total number of arrows that leads to this cell.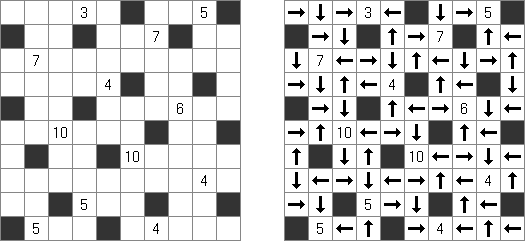
Every Second Turn (also known as "Alternate Corners", "Every Second Breakpoint") is a rectangular or square grid with circles in some cells. The aim is to draw a single continuous non-intersecting loop that visits every cell exactly ones. It makes a 90 degrees turn at every cell with a circle. There is exactly one turn between two consecutive circles that the loop visits.
Mobiriti ("Mobility") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains circles with numbers in some cells. The aim is to blacken some cells of a grid. Cells with circles can not be blacken. A number in a circle indicates how many empty white cells can be reached from that cell by moving horizontally or vertically.
Mubunanba ("Move Number") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains digits in some cells. The goal is to locate some blocks in the grid, having the size of exactly three cells. The grid may contain cells that belong to no one block. Each block contains exactly one digit. A digit indicates the number of the possible directions to move a block.
Terra X consists of a rectangular or square grid divided into regions. The aim is to place a digit from 0 to 9 into each region so that regions with equal numbers cannot share an edge (they may touch each other diagonally). For each grid point where four regions meet, the sum of the digits in those regions must equal 10. (All these grid points are marked with a small black dot.)
Rimotoejji ("Remote Edge") is a logic puzzle created by Naoki Inaba (Japan). The goal is to connect all dots by a single continuous non-intersecting loop. All arrows and crosses are supposed to be contained within the loop. An arrow points in the direction of the longest straight sequence of cells visible from that cell. A cross is placed at the center of more than one longest straight sequences of cells within the loop.
Double Back consists of a rectangular or square grid divided into regions. The aim is to draw a single closed loop of horizontal and vertical segments passing through all white cells. Each region must be visited exactly twice. The grid may contain black cells; the loop cannot pass through a black cell.
Wamuzu ("Worms") is a logic puzzle invented by Naoki Inaba (Japan). It consists of a grid, with circles in some cells. The goal is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. All cells must be used by the lines. All sections of each line must be equal to the length of the cell's side.
Kaero ("Ouchihekaero"; from Japanese, literally "let's go home") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid is divided into regions. The aim is to move some letters horizontally or vertically, so all letters in a region must be the same. The letters cannot cross the tracks of other letters and cannot move over other letters.
Kapama (from Turkish, literally "closing") consists of a rectangular or square grid with diagonal lines in some cells. The goal is to blacken some cells to create pairs of figures (twin shapes). Twin shapes are symmetrical with respect to a diagonal line. Twin shapes are connected with a diagonal line. No two shapes may share an edge. Cells with diagonal lines can not be blacken. Numbers outside the grid show the number of black cells in corresponding row or column.
Yunikumaka ("Unique Marker") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains dots; a dot can be situated in the center of a cell or on a border between neighbouring cells. The aim is to divide a grid on regions having the size of exactly four cells (tetromino). Each region contains exactly one dot either in the center of a cell or on a border between cells. Dots on borders between regions are ignored. Black cells do not belong to any region.
Meandering Numbers (also known as "Count Number", "Worms") is played on a rectangular or square grid divided into regions. A grid may contain numbers in some cells. Each region must be filled with each of the digits from 1 to N, where N is the number of cells in the region. Cells with the same digits must not be orthogonally or diagonally adjacent. Consecutive numbers within the region are orthogonally adjacent. (For each region it must be possible to draw a path that starts at 1 and ends at N, going through each other cell exactly once and in numerically increasing order.)
Yokibunkatsu (from Japanese, literally "container dividing") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains stars in some cells. The goal is to divide the grid into regions of exactly five cells. Each region contains a star. The cells of the region must be foldable to a cube, with the star at the bottom and without the top side ("roof"). Some sections of borders between regions have already been given. The grid may contain cells that belong to no one region.
Scrin ("Screen") is a logic puzzle published by Nikoli. A rectangular or square grid contains circles (empty or with numbers) in some cells. The goal is to divide the grid into rectangular regions. Each region contains not more than one circle. The grid may contain regions without circles. A region must have the same number of cells as a number in a circle. Regions must not share an edge. Regions must form a single non-branching loop where all of them touch each other by corners.
From 1 To X consists of a rectangular or square grid divided into regions. Each region must be filled with each of the numbers from 1 to the number of cells in the room. Same numbers must not be orthogonally adjacent. Numbers outside the grid show the sums of the numbers in corresponding row or column.
Shingoki (from Japanese, literally "traffic lights") is a rectangular or square grid with circles in some cells. The goal is to draw a single continuous non-intersecting loop that passes through all circles. Black circles must be turned upon, white circles must be traveled straight through. In a cell with a gray circle the loop may turn or not. If a circle contains a number, this number indicates the total length of the straight lines going out of the circle.
Stitches consists of a rectangular or square grid divided into regions. The aim is to connect each region with all neighbor regions with exactly one line ("stitch"). A length of each line is one cell (it connects two orthogonally adjacent cells from different regions). A cell may be visited at most one line. A number at the edge of the grid indicates how many line end points must be placed in the corresponding row or column.
Cross+A can solve puzzles with 2, 3 or 4 lines connecting neighbor regions.
Neibadomino ("Neighbour Domino") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains numbers in some cells. The aim is to locate some blocks in the grid, having the size of exactly two cells ("dominoes"), and fill blocks with numbers. The grid may contain cells that belong to no one block. Each number in the grid should be part of a block, indicating the amount of orthogonally adjacent dominoes. Blocks with the same numbers must not be orthogonally adjacent. Blocks must not cover an area of 2 x 2 cells. (The grid may contain 2 x 2 cell area without blocks.)
Jemini ("Jemini Block") is a logic puzzle invented by Naoki Inaba (Japan). A rectangular or square grid contains letters in some cells. The goal is to divide the grid into regions such that each region contains exactly one letter. In regions of the same size, shape and orientation the same letter must be exactly at the same position.
Double Choco is a logic puzzle published by Nikoli. In a rectangular or square grid exactly half of cells are painted gray. The aim is to divide the grid into regions. Each region must contain one area of white cells and one area of gray cells. A pair of areas must be of the same shape and size (the areas may be rotated or mirrored). A number indicates how many cells of the same color the region contains. A region may contain more than one cell with a number (in this case the cells contain the same number).
Konarupu ("Corner Loop") is a logic puzzle invented by Naoki Inaba (Japan). The goal is to create a continuous non-intersecting loop, drawn from one dot to an adjacent dot horizontally or vertically. A number in a cell indicates how many times the loop turns by 90 degrees in dots surrounding this cell.
Gaidoaro ("Guide Arrow") is a logic puzzle created by Naoki Inaba (Japan). A rectangular or square grid contains arrows and a single star. The goal is to blacken some cells so that the white cells must be connected horizontally or vertically. Blackened cells should not share an edge. Cells with arrows or a star cannot be blackened. An arrow indicates the direction in which you must move to reach a star by only going through white cells (there must be only one way from any white cell to reach a cell with a star).
Mid-Loop is a logic puzzle published by Nikoli. A rectangular or square grid contains dots; a dot can be situated in the center of a cell or on a border between neighbouring cells. The aim is to draw a single continuous non-intersecting loop that properly passes through all dots. Dots must be traveled straight through. Segments of a straight line going out of a dot must be equal.
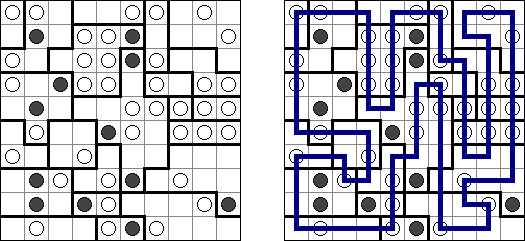
Dotchi-Loop is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. A grid contains white and black circles in some cells. The goal is to draw a single non-intersecting loop. The loop must visit all cells with white circles; the loop cannot pass through a black circle. The line either travels straight through all the white circles, or makes a 90 degrees turn at all the white circles in a region.
Trinairo is a logic puzzle invented by Leo de Winter (Netherlands). The objective is to fill a 9 x 9 grid with letters so that each row and each column contains three letters A, three letters B and three letters C. If a cell is marked with other color, a letter in the cell differs from letters in all orthogonally adjacent cells.
Detour is a logic puzzle. It contains a rectangular or square grid divided into regions. The goal is to draw a single continuous non-intersecting loop that visits every cell exactly ones. Each number in a region indicates the number of times the loop turns in the region.
Balance Loop is a logic puzzle created by Prasanna Seshadri (India). A rectangular or square grid contains black and white circles in some cells. The aim is to draw a single continuous non-intersecting loop that visits all cells with circles. Loop segments extending from a white circle are of equal length, while the loop segments extending from a black circle are not. If a cirlce contains a number, it indicates the sum of the loop segment lengths on both sides of the circle.
Turf is a logic puzzle invented by John Bulten (USA). A rectangular or square grid contains numbers in some cells. The goal is to shade some cells so that the grid will be divided into gray and white regions. Each region must contain at least one number. This number indicates the size of a region. If a region contains any other cell with a number, it represents how many surrounding cells are white, including itself and diagonal ones.
SquarO is a logic puzzle similar to Minesweeper. A rectangular or square grid contains dots on intersections of lines. A number in a cell indicates how many of the four surrounding dots are black.
Chiyotsui (from Japanese, literally "door hinge") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:
Black cells form areas. Each area spans exactly two regions, its parts are symmetrical with respect to the region border. A cell with a number indicates how many cells in the region must be blackened. No two black areas may share an edge.
Aqre is a logic puzzle invented by Eric Fox (USA). A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid that all black cells form one orthogonally connected area. A cell with a number indicates how many cells in the region must be blackened. In regions without a number any amount of cells may be blackened (all cells may stay white). There cannot be a run of more than three black or white cells in the grid.
Geradeweg ("Straight Loop") is a logic puzzle. A rectangular or square grid contains circles with numbers in some cells. The task is to draw a single closed non-intersecting loop that passes through all circles. The number indicates the length of the straight segment passed through the circle. If the loop turns in a number cell, both straight segments must have the same length as the number indicates.
Kuroclone is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The aim is to blacken some cells of a grid. Each region must contain two areas of black cells: this pair of areas must be of the same shape and size (the areas may be rotated or mirrored). Cells with numbers are always white. The arrow points to an adjacent cell that belongs to a black area. The number indicates the size of this area. When two cells are orthogonally adjacent across a region boundary, at least one cell must be white.
Yajisan-Sokoban is a logic puzzle invented by Jamie Hargrove. A rectangular or square grid contains gray squares. The task is to move the gray squares vertically or horizontally (some squares may stay unshifted). Gray squares cannot cross the tracks of other gray squares and cannot move over other squares (gray squares can pass through numbered cells). A cell containing a number and an arrow represents how many gray squares are in the row or column pointed at by the arrow. If there is a gray square on top of a numbered cell, it plays no further role in the puzzle, and may be true or false. If a gray square passes through a cell with a number and an arrow, this numbered cell provides true information.
Line Segment is a logic puzzle invented by Erich Friedman (USA). The task is to draw line segments that pass through exactly 3 or 4 consecutive cells. The line segments can only be horizontal (H), vertical (V), or diagonal (D). Each cell must be visited exactly once. A cell with a letter contains a line segment with that orientation.
Raneko ("Ranekomappu"; from Japanese, literally "cat habitat map") is a logic puzzle published by Nikoli. A rectangular or square grid contains circles (with numbers or empty). The goal is to divide the grid into regions. Each region contains one circle ("cat"). A circle with a number indicates the size of a region. A grid may contain black cells. The number in a black cell indicates how many regions share an edge with that black cell.
Factorism ("Find the Factors") is a logic puzzle invented by Iva Sallay (USA). The goal is to place numbers from 1 to N across the top and down the left of the square grid N x N. A number in a cell indicates the product of numbers outside the grid in the corresponding row and column.
Akiperago ("Archipelago") is a logic puzzle published by Nikoli. A rectangular or square grid contains black cells; some of them contains numbers. The goal is to blacken some cells of a grid according to the following rules:
The black cells form "islands". No two islands may share an edge; islands may be connected through their corners. If an island contains a numbered cell, this number represents the amount of black cells in the island. An island may contain few numbered cells (all numbers will be the same inside an island). All islands form "archipelagos". An archipelago is a group of two or more islands, connected through their corners. If an archipelago contains N islands, they will be from 1 to N cells (not necessarily in that order).
Yakazu is a logic puzzle invented by Patrick Tirone. A rectangular or square grid is partially divided by black cells into compartments. The aim is to fill all white cells with the numbers. Each compartment, vertically or horizontally, must contain a set of consecutive numbers, but in any order (for example: 4-1-3-2). Each compartment of two cells or more must contain all the numbers starting from 1.
Miraringutairu ("Mirroring Tile") is a logic puzzle published by Nikoli. A rectangular or square grid contains black cells; some of them contain numbers. The goal is to locate blocks of black cells in the grid. Each numbered cell indicates the total number of black cells in the block (a block may contain few numbered cells). The grid may contain blocks without numbers. No two blocks may share an edge, but each block must be connected with at least one another block of the same size and shape through their corners (blocks may be rotated or mirrored).

Heyablock ("Heyawake-Block") is a logic puzzle invented by Atsumi Hirose (Japan). A rectangular or square grid is divided into regions. The aim is to blacken some cells of a grid according to the following rules:
All black cells in a region must be connected. A cell with a number indicates how many cells in the region must be blackened. In regions without a number any amount of cells may be blackened (at least one). When two cells are orthogonally adjacent across a region boundary, at least one cell must be white. All white cells form one orthogonally connected area. A line of connected white cells cannot go through two or more region borders.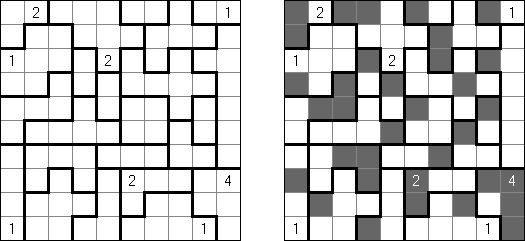
Choco Banana is a logic puzzle published by Nikoli. A rectangular or square grid contains numbers in some cells. The goal is to blacken some cells of a grid. An area of black cells must form a rectangle or square. An area of white cells must not form a rectangle or square. If a black or white area contains a number, it indicates the size of this area. An area may contain more than one cell with a number.
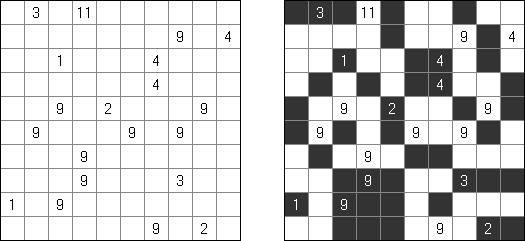
Wataridori (from Japanese, literally "migratory birds") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. A grid contains circles (empty or with numbers) in some cells. The aim is to connect circles in pairs by drawing a line that goes horizontally and vertically through the centers of cells. A cell may be visited by a line at most once. A line may connect circles with equal numbers, empty circles, or a line may be drawn between an empty circle and a circle with a number. A number in a circle indicates how many regions are visited by the line. A region may be visited by the line at most once.
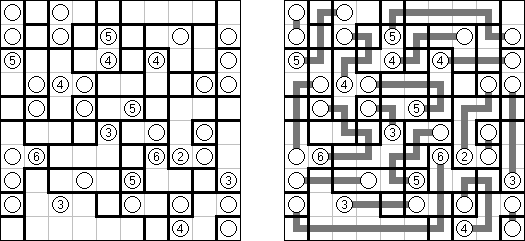
Chenburo ("Chain Block") is a logic puzzle published by Nikoli. A grid contains numbers or question marks in some cells. The aim is to blacken some cells of a grid according to the following rules:
The black cells form blocks. No blocks touch each other horizontally or vertically (only diagonally). A number represents the amount of black cells in the block. Question marks can be used instead of clue numbers. Each question mark can represent any nonzero integer. Each block contains exactly one number or a question mark. All blocks form "chains". A chain is a group of two or more blocks, connected through their corners. Two blocks belonging to the same chain may not have the same shape and size, counting rotations and reflections as the same.
Wanrumuwandoa ("One Room One Door") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions ("rooms"). A region may contain a cell with a number. The goal is to blacken some cells of a grid according to the following rules:
A cell with a number indicates how many cells in the region must be blackened. In regions without a number any amount of cells may be blackened. Blackened cells should not share an edge. All the white cells must be connected inside a region (it's possible for a region to have no white cells). If two white cells are orthogonally adjacent across a region boundary, they form a "door". There can be no more than one door between any two regions. All the white cells must form an orthogonally continuous area.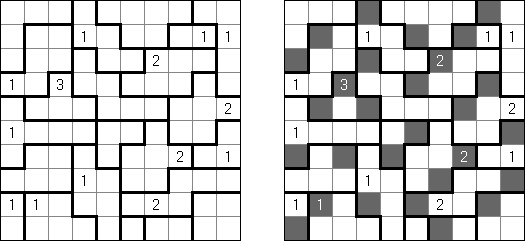
Haisu ("House") is a logic puzzle invented by William Hu. A square or rectangular grid is divided into regions. The aim is to draw a line ("path") from S (start) to G (goal) that goes through all cells. The line cannot cross itself. The line can visit each region more than once. When the line passes over a cell with a big number N, it is on its Nth entry to the region. If a region has a small number n in the top left corner, the line must visit this region a total of n times.
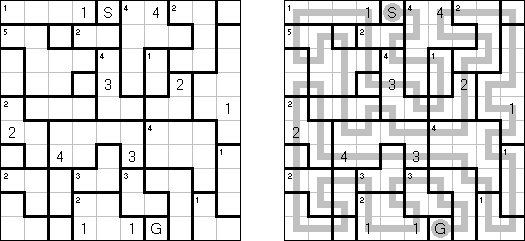
Obitaru (from Japanese, literally "orbital") is a logic puzzle published by Nikoli. A grid contains white and black circles; black circles may contain numbers. The goal is to draw square or rectangular loops ("belts"). The loops may cross each other, but parallel lines cannot pass through the same cell. Loops must pass through all white cells. There may be loops that do not pass through any white circle. A black circle should be inside exactly one loop (there can be no more than one black circle inside the loop). If the black circle contains a number, it will be equal to the number of white circles through which the loop passes around this black circle.
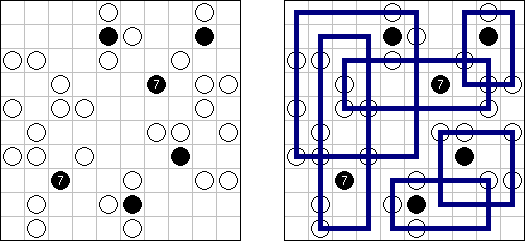
Square Jam is a logic puzzle. A rectangular or square grid contains numbers in some cells. The aim is to divide the grid into square regions. A cell with a number indicates the side length of a region. A region may contain any amount of numbered cells. The grid may contain regions without numbers. A grid dot must not be shared by the corners of four regions.
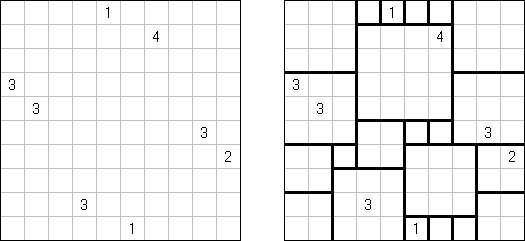
Cocktail Lamp ("Kakuteruranpu") is a logic puzzle. A rectangular or square grid is divided into regions. The goal is to blacken some cells of a grid according to the following rules:
All black cells in a region must be connected horizontally or vertically (they form a "block"). A cell with a number indicates how many cells in the region must be blackened. In a region without a number any amount of cells may be blackened (all cells may stay white). When two cells are orthogonally adjacent across a region boundary, at least one cell must be white. All blocks of black cells must be connected to each other through their corners. No 2 x 2 cell area within the grid can contain all black cells.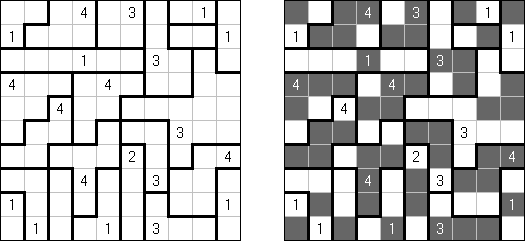
Kazoku ("Kazoku shashin"; from Japanese, literally "family photo") is a logic puzzle. A rectangular or square grid contains black circles in some cells; some circles may contain numbers or question marks. Also, some cells may contain numbers or question marks. The aim is to divide the grid into rectangular regions such that each region contains exactly one number or question mark. A number indicates how many black circles the region contains. The region with a question mark may conatin any amount of black circles (at least one). Orthogonally adjacent circles must belong to the same region.
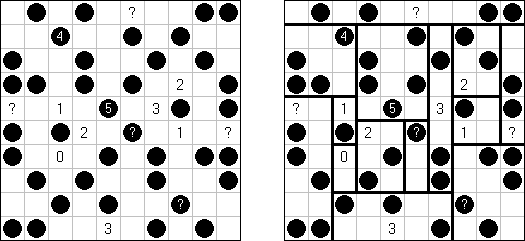
Tontonbeya (from Japanese, literally "gambler") is a logic puzzle published by Nikoli. A rectangular or square grid is divided into regions. The goal is to fill in each cell with figures: squares, circles, triangles. A region may contain any types of figures, but if they are of different types, the number of figures of each type should be the same. All figures of the same type in a region must be connected horizontally or vertically (they form a "block"). Each block of the same figures within one region must be adjacent to a block of the same figures in another region. There should not be a block that is adjacent to two or more blocks of the same figures in other regions.
Context is a rectangular or square grid with numbers in some cells. The aim is to blacken cells of a grid according to the following rules:
All the white cells must be connected horizontally or vertically. A cell with a number can be blacken. Two black cells must not be orthogonally adjacent. The number in a white cell indicates the number of orthogonally adjacent black cells. The number in a black cell indicates the number of diagonally adjacent black cells.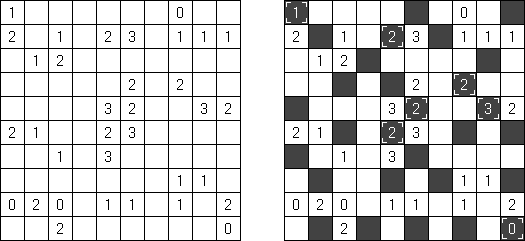
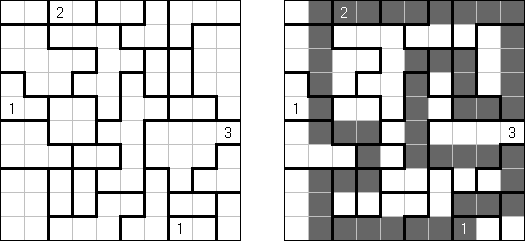
Circles and Squares is a logic puzzle. A square or rectangular grid contains black and white circles. The aim is to blacken cells of a grid according to the following rules:
Cells with black circles must be blacken. Cells with white circles cannot be blacken. The black cells divide the grid in areas of white cells. These areas must be square. No 2 x 2 cell area within the grid can have the black color. All the black cells must form an orthogonally continuous area.
Putteria (from Japanese, "put into an area") consists of a grid divided on regions. The goal is to place a number into each region. A number is equal to the size of the region. No number may appear twice in any row or column. Cells with numbers must not be orthogonally adjacent. A cell with a cross cannot contain a number.

Summandum (from Latin, "summarize") is a square grid with numbers in some cells. The aim is to place numbers from 0 to N across the top and down the left of the square grid. A number in a cell indicates the sum of numbers outside the grid in the corresponding row and column.

Word Finder("单词搜索", "Word Search","Word Seek","Word Sleuth","Mystery Word")使用正方形或长方形的格网,内部有字母。需要在格网中找单词。单词的字母要用折线迷惑起来;这条线只弯曲90度。每一个字母只能使用一次。
为了制作谜题,先需要遴荐单词。而且,也不错遴荐谬误词,解完谜题以后,未使用的字母就组成谬误词。
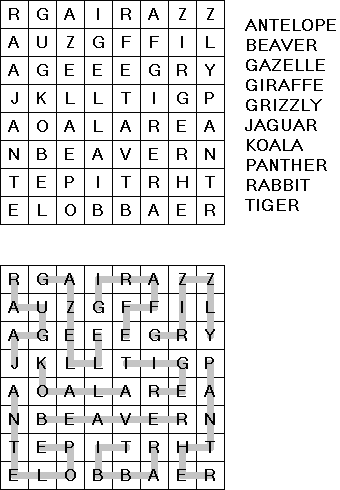
Nine Letters - 是 Word Finder 单词的谜题的变种。使用正方形的格网,分为小格(3×3),内部有字母。需要在格网中找9个字母的单词。

Spider Web - 有被一条线迷惑起来的圈儿。在圆圈中有字母。需要找包括谬误单词字母的圈儿的连气儿序列。
Maze (迷宫) - 是一个犬牙交错的说念路组成的结构。需要找到两个标出的点之间的旅途。缱绻神秘道使您不错创建苟且阵势的迷宫,不仅是长方形或正方形。
 我想要插插插综合网
我想要插插插综合网